Quest 4 - Paths and Equality

If you have come here from Fundamental Group of the Circle then have a look at the overview to understand the philosophy of trinitarianism.

So far in trinitarianism there has been no mention of “equality”; we have never said what it meant for two types or two terms to be “the same”. However, in Fundamental Group of the Circle we have expressed what it means for two spaces to look the same, by creating a path from one space to the next (usually by an isomorphism). Indeed we will take this to be our definition of (internal) equality.

We will often adopt the geometric perspective, but change perspectives when appropriate.

Universe levels

In the solutions we always use Type u, but just write Type here. There is no conceptual difference with using an arbitrary universe, but in practice we want to be as general as possible.

It is useful to stick to just using Type, and realise why it is not general enough when problems arise.

Part 0 - The Identity Type

The construction

Given A : Type and x y : A we have a type Id x y : Type, called the identity type of x to y.

data Id {A : Type} : (x y : A) → Type where

  rfl : {x : A} → Id x x

The construction takes in (implicit) argument A : Type, then for each pair of points x y : A it returns a space Id x y with interpretations :

Id x y is the proposition “x equals y (internally)” and for every x, we have a proof rfl x that “x is equal to itself (internally)”. (Hence the name rfl, which is short for reflexivity.)
The only recipe for the construction Id x y is given when x is the same recipe as y.
Id x y is the space of paths from x to y, i.e. points in the space are paths from x to y in A. For every point x in A, there is the constant path rfl x at x.
Id is a bundle over A × A and the diagonal map A → A × A, taking x ↦ (x , x), factors through Id → A × A (viewing Id as the total space Σ (A × A) Id).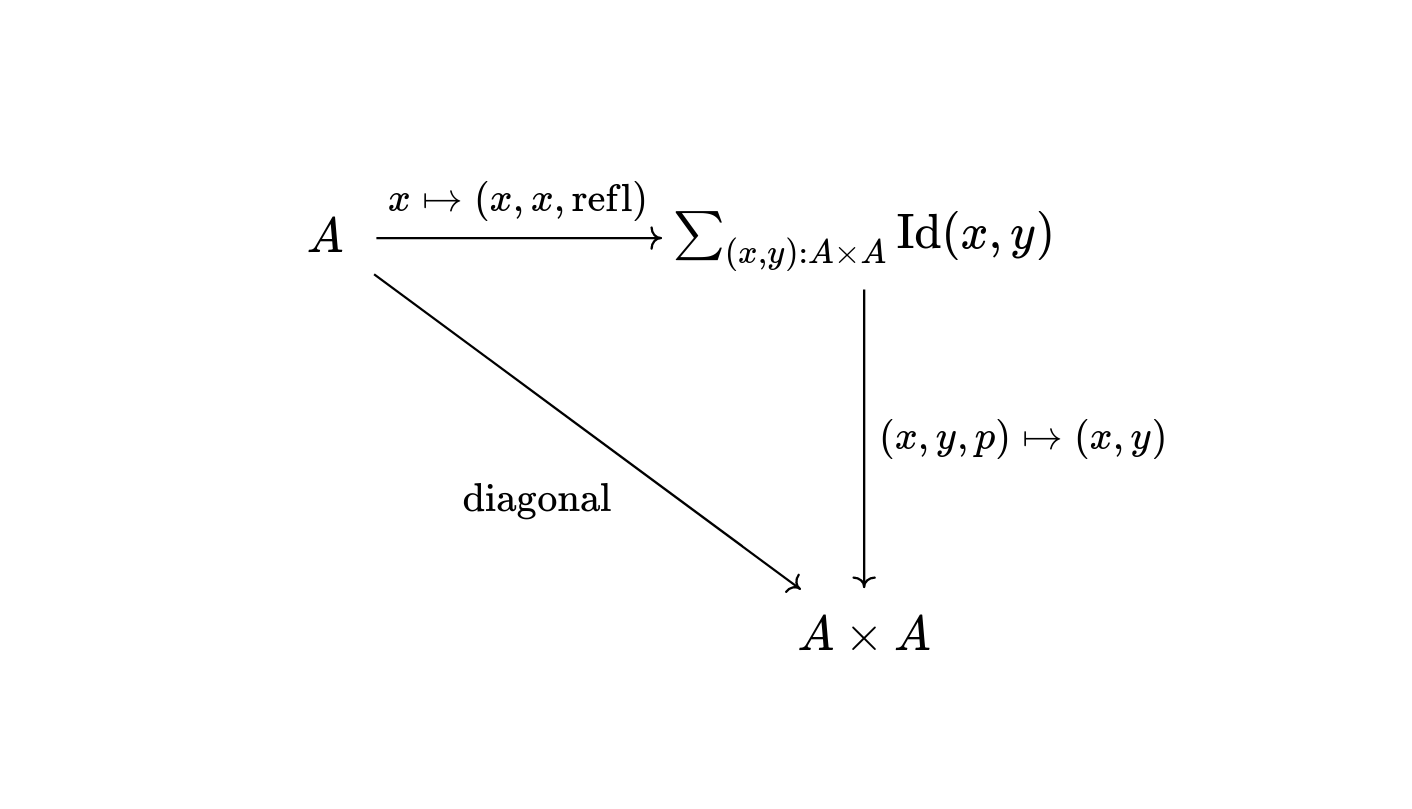

Write this up in 0Trinitarinism/Quest4.agda. We recommend you first try having the explicit argument for rfl in rfl : (x : A) → Id x x, so you can see exactly what is going on, but we will use rfl with an implicit argument rfl : {x : A} → Id x x.

Internal versus external equality

In the first perspective use the word “internal” since there is also the notion of “external equality” that we want to distinguish. In short x and y are externally equal if the computer believes they are the same term, i.e. the string of symbols they simplify (normalise) to are exactly the same.

If two terms are externally equal then they are internally equal, and the proof that they are internally equal is rfl. However, having a proof p : Id x y is not enough for the computer to recognise x as the same term as y.

Exercise - Symmetry

For Id to be a good notion of equality it should at least be an equivalence relation. It is reflexive by having rfl in the definition. We show that it is symmetric:

idSym : (A : Type) (x y : A) → Id x y → Id y x
idSym = {!!}

This has interpretations:

Equality is symmetric
We can turn recipes for the construction Id x y into recipes for the construction Id y x
Paths can be reversed

Add this to the file 0Trinitarianism/Quest4.agda and try showing it. We give a detailed explanation in the hints and solution.

Hint 0

Assume we have a space A, points x y : A and a proof of equality / recipe / path p : Id x y. It may help to view Id x y as a construction to think about how to proceed.

Hint 1

If you case on p : Id x y then you should see the following

idSym : (A : Type) (x y : A) → Id x y → Id y x
idSym A x .x rfl = {!!}

We interpret this as

If x and y are equal by proof p and we want to show something about x y and p, then it suffices to consider the case when they are externally equal; that y is literally the term x and p is rfl.
The only recipe we had for the construction Id x y is rfl, so we should be able to reduce to this case.
To map out of Id, viewed as a total space, it suffices to map out of the diagonal.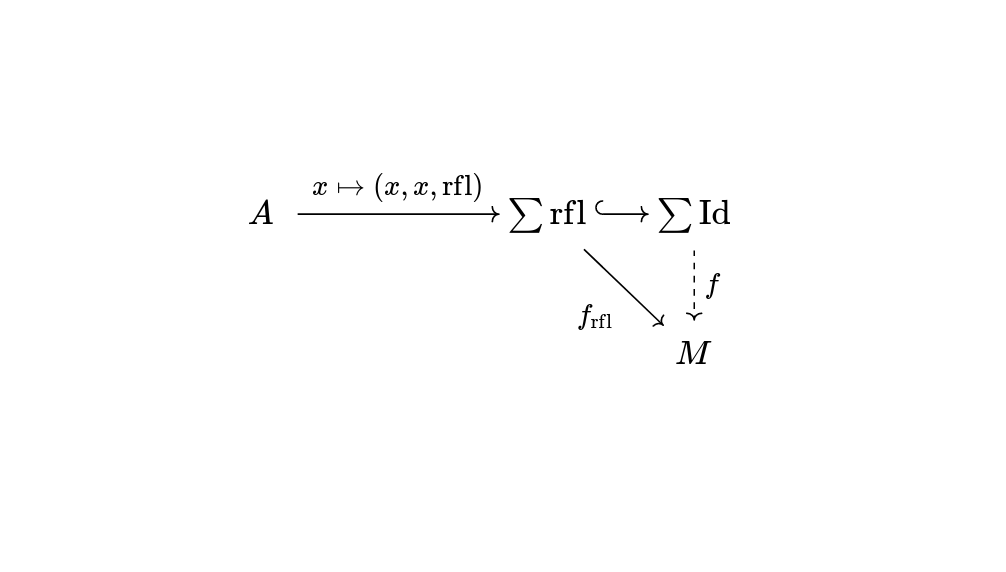

Solution

Since we have reduced to the case for when both points are x, we can simply supply a point in Id x x. There is an obvious one.

idSym : (A : Type) (x y : A) → Id x y → Id y x
idSym A x .x rfl = rfl

The Geometric Perspective

We have not included a justification via the geometric perspective. This is because intuitively it’s not quite obvious that to map out of the space of paths it suffices to map the constant path. We justify the mapping out property geometrically in a side quest.

We can also make the relevant arguments implicit. We will be using the following version from now on :

Sym : {A : Type} {x y : A} → Id x y → Id y x

Exercise - Transitivity

In 0Trinitarianism/Quest4.agda, try to formalize (and then prove) the following interpretations of the same statement :

Id is transitive, which says if Id x y and Id y z both hold, then so does Id x z.
recipes for Id x y and Id y z can be made into recipes for Id x z.
paths can be concatenated

The statement

idTrans : (A : Type) (x y z : A) → Id x y → Id y z → Id x z
idTrans = {!!}

You may wish to make some of the arguments implicit. We could also introduce notation that suggests concatenation:

_*_ : {A : Type} {x y z : A} → Id x y → Id y z → Id x z
_*_ = {!!}

We will use _*_.

Hints

There are multiple ways of defining this. Assuming p : Id x y and q : Id y z we could

case on p and identify x and y
case on q and identify y and z
case on both p and q, identifying all three

Solutions

_*_ : {A : Type} {x y z : A} → Id x y → Id y z → Id x z
rfl * q = q

_*0_ : {A : Type} {x y z : A} → Id x y → Id y z → Id x z
p *0 rfl = p

_*1_ : {A : Type} {x y z : A} → Id x y → Id y z → Id x z
rfl *1 rfl = rfl

These three definitions will work slightly differently in practice. We will use the first of the three, but you can use whichever you prefer.

Exercise - Groupoid Laws

The identity type satisfies some further properties, which you can formalize then prove. You may notice that they look almost like the axioms of a group, except a bit bigger - for example there is not just a single identity element (refl works at each point in the space).

Note that our solutions may differ to yours depending on your choice of how to define transitivity / concatenation.

concatenating rfl on the left and right does nothing,
The statements
```
rfl* : {x y : A} (p : Id x y) → Id (rfl * p) p
rfl* = {!!}

*rfl : {x y : A} (p : Id x y) → Id (p * rfl) p
*rfl = {!!}
```
The first says if you concatenate rfl on the left then it is equal to the original path.
Solutions
```
rfl* : {x y : A} (p : Id x y) → Id (rfl * p) p
rfl* p = rfl

*rfl : {x y : A} (p : Id x y) → Id (p * rfl) p
*rfl rfl = rfl
```
Note that we needed to case on the path in the second proof due to our definition of concatenation.
Tip

If you are tired of writing {A : Type} {x y : A} each time you can stick
```
private
  variable
    A : Type
    x y : A
```
at the beginning of your agda file, and it will assume A, x and y implicitly whenever they are mentioned. Make sure it is indented correctly. Beware that anything declared like this will be an implicit argument.

We also recommend reading about the module system in agda.

concatenating a path p with Sym p on the left and right gives rfl.

The statements

Sym* : {A : Type} {x y : A} (p : Id x y) → Id (Sym p * p) rfl
Sym* = {!!}

*Sym : {A : Type} {x y : A} (p : Id x y) → Id (p * Sym p) rfl
*Sym = {!!}

Solutions

Sym* : {A : Type} {x y : A} (p : Id x y) → Id (Sym p * p) rfl
Sym* rfl = rfl

*Sym : {A : Type} {x y : A} (p : Id x y) → Id (p * Sym p) rfl
*Sym rfl = rfl

Concatenation is associative

The statement

Assoc : {A : Type} {w x y z : A} (p : Id w x) (q : Id x y) (r : Id y z)
        → Id ((p * q) * r) (p * (q * r))
Assoc = {!!}

Solution

Assoc : {A : Type} {w x y z : A} (p : Id w x) (q : Id x y) (r : Id y z)
        → Id ((p * q) * r) (p * (q * r))
Assoc rfl q r = rfl

These axioms say that any type is a groupoid, with the above structure. This aligns well with the geometric perspective of types : in classical homotopy theory any space has a groupoid structure and any groupoid can be made into a space.

Recursor - The Mapping Out Property of `Id`

We may wish to extract the way we have made maps out of the identity type :

Mapping out property of Id

Assuming a space A and a point x : A. Given a bundle M : (y : A) (p : Id x y) → Type over the “space of paths out of x”, in order to make a map {y : A} (p : Id x y) → M y p, it suffices to give a point in M x refl. This is traditionally called the “recursor” of Id. (We have still not justified this geometrically.)

For example, in order to prove *Sym : {A : Type} {x y : A} (p : Id x y) → Id (p * Sym p) rfl, we would choose our bundle M to be λ y p → Id (p * Sym p) rfl, taking each y : A and p : Id x y to the space of paths from (p * Sym p) to rfl in Id x x. When we proved this in the previous section, agda figured out what M needed to be and just asked for a proof of the case M x rfl.

In 0Trinitarianism/Quest4.agda, try formalising the mapping out property, and call it outOfId.

The statement

outOfId : (M : (y : A) → Id x y → Type) → M x rfl
  → {y : A} (p : Id x y) → M y p
outOfId = {!!}

Note that we have used the symbol y in the type of M, but it really is just a local variable and will not appear outside that bracket. We made the last y an implicit argument, since p contains the data of y.

Solution

outOfId : (M : (y : A) → Id x y → Type) → M x rfl
  → {y : A} (p : Id x y) → M y p
outOfId M h rfl = h

The proof is of course just casing on the path p, as we are trying to extract that idea.

Part 1 - The Path Space

If you came here from the quest on Fundamental Group of the Circle then you may be wondering why there has not been any mention of the path space x ≡ y. The reason is that whilst ≡ and Id are meant to represent the same idea, the implementation of Id is simple - we were able to write it down; whereas the implementation of ≡ is “external”, and purely existing in cubical agda. In this part we will show that the two are “the same” as spaces i.e. isomorphic, and after this we will only use ≡ for equality and paths (as is the convention in the cubical library).

We assert the following three axioms for the path space (we will add another (univalence) in later):

If x is a point in some space then refl is a proof of x ≡ x.

The mapping out property, called J :

J : (M : (y : A) → x ≡ y → Type) → M x refl
  → {y : A} (p : x ≡ y) → M y p

This looks exactly like outOfId.

The mapping out property applied to refl :
```
JRefl : (M : (y : A) → x ≡ y → Type) (h : M x refl)
  → J M h refl ≡ h
```
This says that when we feed refl to J M h it indeed gives us what we expect - something equal to h. Unfortunately, though (given correct M and h) outOfId M h rfl would externally be equal to h, J M h refl is not externally equal to h, but this is a cubical agda issue and not a HoTT issue.

Paths versus `Id`

The goal

Given two points x y : A, the path type x ≡ y is isomorphic to Id x y. We introduce isomorphism in Quest 0 of the Fundamental Group arc.

So we are trying to show

Path≅Id : (x ≡ y) ≅ (Id x y)
Path≅Id = {!!}

This involves a lot of small steps, which we split up into hints.

Hint 0

“Refining” in the hole will make it ask for the four components in the proof of an isomorphism.

Path≡Id : (x ≡ y) ≅ (Id x y)
Path≡Id = iso {!!} {!!} {!!} {!!}

Hint 1

To make an isomorphism we need to make maps forwards and backwards, these go in the first two holes.

Path→Id : x ≡ y → Id x y
Path→Id = {!!}

Id→Path : Id x y → x ≡ y
Id→Path = {!!}

Hint 2

To make the map forwards we will need to use J - the mapping out property of the path space. To map backwards we can use outOfId or just case on a path.

Path→Id : x ≡ y → Id x y
Path→Id {A} {x} = J {!!} {!!}

Id→Path : Id x y → x ≡ y
Id→Path rfl = {!!}

For the first, in order to state the motive we need the implicit arguments A and x.

Solution

Path→Id : x ≡ y → Id x y
Path→Id {A} {x} = J (λ y p → Id x y) rfl

Id→Path : Id x y → x ≡ y
Id→Path rfl = refl

Hint 3

Filling in what we have so far and extracting the relevant lemmas we have

Path≅Id : (x ≡ y) ≅ (Id x y)
Path≅Id {A} {x} {y} = iso Path→Id Id→Path rightInv leftInv where

   rightInv : section (Path→Id {A} {x} {y}) Id→Path
   rightInv = {!!}

   leftInv : retract (Path→Id {A} {x} {y}) Id→Path
   leftInv = {!!}

We have filled in the necessary implicit arguments for you.

Hint 4

Since section Path→Id Id→Path will first take in p : Id x y we give such a p and case on it. It should of course just turn into rfl.

Since retract Path→Id Id→Path will first take in p : x ≡ y we directly use J.

Path≅Id : (x ≡ y) ≡ (Id x y)
Path≅Id {A} {x} {y} = iso Path→Id Id→Path rightInv leftInv where

   rightInv : section (Path→Id {A} {x} {y}) Id→Path
   rightInv rfl = {!!}

   leftInv : retract (Path→Id {A} {x} {y}) Id→Path
   leftInv = J {!!} {!!}

Hint 5

Checking the goal for rightInv we should see it requires a point in Path→Id (λ _ → x) ≡ rfl, which is the same as Path→Id refl ≡ rfl. What’s happened is agda knows that Id→Path rfl is just refl (they are externally equal), so instead of asking for a point of Path→Id (Id→Path rfl) ≡ rfl it just asks for a proof of the reduced version. (In our heads we reduce (λ _ → x) to refl but agda does the opposite.)

We extract the above result as a lemma :

Path→IdRefl : Path→Id (refl {x = x}) ≡ rfl
Path→IdRefl = {!!}

Solution

Since Path→Id uses J, the only thing we can do here is use JRefl :

Path→IdRefl : Path→Id (refl {x = x}) ≡ rfl
Path→IdRefl {x = x} = JRefl (λ y p → Id x y) rfl

Hint 6

For leftInv, giving the correct motive requires knowing what retract says. It should look like

leftInv : retract (Path→Id {A} {x} {y}) Id→Path
leftInv = J (λ y p → Id→Path (Path→Id p) ≡ p) {!!}

Checking the goal we should see it requires a point in Id→Path (Path→Id refl) ≡ refl. It should be that we just can replace Path→Id refl with rfl using our lemma Path→IdRefl : Path→Id refl ≡ rfl - but we haven’t proven anything about paths yet! Let us do so now : if f : A → B is a function (in our case Id→Path) then if two of its inputs are the same x ≡ y then so are the outputs, f x ≡ f y.

cong : (f : A → B) (p : x ≡ y) → f x ≡ f y
cong = {!!}

We can prove this directly using J or via Id. (We call it cong' to avoid clashing with the library’s version)

Solutions

Cong : (f : A → B) → Id x y → Id (f x) (f y)
Cong f rfl = rfl

cong' : (f : A → B) (p : x ≡ y) → f x ≡ f y
cong' {x = x} f = J (λ y p → f x ≡ f y) refl

cong'' : (f : A → B) (p : x ≡ y) → f x ≡ f y
cong'' f p = Id→Path (Cong f (Path→Id p))

From now on we will just use cong from the library, but you can try to continue with your own version. Now using cong we can define leftInv. Noting that externally Id→Path rfl is the same as refl, we just need to show that Id→Path (Path→Id refl) ≡ Id→Path rfl.

Solution

leftInv : retract (Path→Id {A} {x} {y}) Id→Path
leftInv = J (λ y p → Id→Path (Path→Id p) ≡ p) (cong (λ p → Id→Path p) Path→IdRefl)

Concluding that the two types are isomorphic is a good reason to accept them as “the same” in the sense that if two spaces are isomorphic then they share the same properties, because isomorphism should interact nicely with other constructions. We expand upon this point in Part 3 - Univalence.

Part 2 - Properties of the Path Space

In Fundamental Group of the Circle we assume a couple of results about the path space, which we list here :

The basics : We can make sym (the analogue of Sym) and composition of paths (called _∙_); we can show that paths also satisfy groupoid laws.
We have already made cong in the previous part (in Hint 6).
The function pathToFun which takes a path between spaces and converts it to a function between the spaces, following points along the path of spaces.
The function endPt which follows a path along a bundle.

Some of these properties are what Homotopy Type theorists believe to be the absolute minimal necessary philosophical foundations for considering paths to be a good notion of equality :

refl, sym and _∙_ give us that it is an equivalence relation
cong tells us that any function respects equality.
endPt and pathToFun approximately say that any predicate / family / bundle B : A → Type respects equality.

The Basics

The direct proof of these are a good exercise on J, or can be accomplished by porting over results from the identity type using Path→Id and Id→Path. We won’t go through each proof, but it is worth noting that since equalities tend to be non-external, a little more work is required. To see solutions for this, please see 0Trinitarianism/Quest4Solutions.agda.

Chains of Equalities

Something that will help organizing the above proofs and work later on is a notation for composition that suggests a “chain of equalities”. Let’s say that we want to show that a + (b + c) ≡ c + (a + b) for naturals a b c : ℕ. Then classically one might write

  a + (b + c)
≡ by associativity
  (a + b) + c
≡ by commutativity
  c + (a + b)

In agda we would have both proofs of associativity and commutativity. Let’s call them ha and hc (in practice they would probably be something like +assoc a b c and +comm (a + b) c). Then using some cleverly defined notation, we can write in agda

example : (a b c : ℕ) → a + (b + c) ≡ c + (a + b)
example a b c =
    a + (b + c)
  ≡⟨ ha ⟩
    (a + b) + c
  ≡⟨ hc ⟩
    c + (a + b)
  ∎

One you define _∙_ for composition of paths, you can get access to this notation by including the following code. Try figuring out why it works.

_≡⟨_⟩_ : (x : A) → x ≡ y → y ≡ z → x ≡ z -- input \< and \>
_ ≡⟨ x≡y ⟩ y≡z = x≡y ∙ y≡z

_∎ : (x : A) → x ≡ x -- input \qed
_ ∎ = refl

infixr 30 _∙_
infix  3 _∎
infixr 2 _≡⟨_⟩_

All of this is included in the solutions file.

`pathToFun`

The function pathToFun (originally called transport in the cubical library) has the following interpretations :

If two propositions are equal then one implies the other.
If two constructions can be identified then we can transport recipes of A over to recipes of B
If two spaces look the same / if there is a path between spaces in the space of spaces then we can map one to the other (it turns out that we can make pathToFun always give us an isomorphism).

Try formalizing and defining pathToFun in 0Trinitarianism/Quest4.agda.

The Statement

pathToFun : A ≡ B → A → B

Hint 0

Use J to reduce this to finding a map A → A, and choose the identity map.

Solution

id : A → A
id x = x

pathToFun : A ≡ B → A → B
pathToFun {A} = J (λ B p → (A → B)) id

Show that pathToFun sends refl to the identity map.

The Statement

pathToFunRefl : pathToFun (refl {x = A}) ≡ id
pathToFunRefl = {!!}

Solutions

Since the only thing we know about J is how it computes on refl, we apply that :

pathToFunRefl : pathToFun (refl {x = A}) ≡ id
pathToFunRefl {A} = JRefl (λ B p → (A → B)) id

We might want to also make pathToFunReflx - which says what pathToFun refl does at each point.

Solution

pathToFunReflx : (x : A) → pathToFun (refl {x = A}) x ≡ x
pathToFunReflx x = cong (λ f → f x) pathToFunRefl

`endPt`

The function endPt (originally called subst in the cubical library) has the following meanings :

If B is a predicate on A and x ≡ y are equal terms of A then B x implies B y. “We can substitute x for y in the proof of B x”.
If B is a family of constructions dependent on terms of A and x ≡ y are identified recipes of A, then recipes of B x can be turned into recipes of B y. “We can substitute the recipe x for y in the recipe for B x”.
If B is a bundle over the space A and we have a path x ≡ y between points in A, then we can follow any “lifted path” starting at some bx : B x to find its end point by : B y.

Predicates / families / bundles respect paths

If we have a predicate / family / bundle B as above and an equality x ≡ y in A, then we know that cong will give us an equality of spaces B x ≡ B y. However, only in the presence of pathToFun is this equality any use - surely if two spaces are equal then we should be able to transport points from one to the other. Hence endPt / pathToFun (often both referred to as transport) justify the statement “predicates / families / bundles” respect paths.

Try to formalize and prove endPt in 0Trinitarianism/Quest4.agda. Then show that it sends refl to what we expect.

Solutions

One option it is a raw application of J.

endPt : (B : A → Type) (p : x ≡ y) → B x → B y
endPt {x = x} B = J (λ y p → B x → B y) id

endPtRefl : (B : A → Type) → endPt B (refl {x = x}) ≡ id
endPtRefl {x = x} B = JRefl ((λ y p → B x → B y)) id

We could also use cong and pathToFun as described above, however due to size issues that we have not addressed in our insufficiently general definition of cong, we have used the library’s version of cong. (Outside this quest we will be using the library’s version of these definitions.)

endPt' : (B : A → Type) (p : x ≡ y) → B x → B y
endPt' B p = pathToFun (cong B p )

Part 3 - Univalence

Paths on Other Constructions

The path space tends to interact nicely with other constructions. We give a list of examples here to demonstrate this point :

For points (a0 , b0) (a1 , b1) : A × B in the product of two spaces we have that (a0 , b0) ≡ (a1 , b1) is “the same” space as the product of path spaces (a0 ≡ a1) × (b0 ≡ b1). Formally we express “the same” using an isomorphism :
```
Path× : {A B : Type} (a0 a1 : A) (b0 b1 : B) → (_≡_ {A × B} ( a0 , b0 ) ( a1 , b1 )) ≅ ((a0 ≡ a1) × (b0 ≡ b1))
```
where we have some kind of product of spaces (however you wish to define it). We give a proof of this in Quest4Solutions; it is quite long but a good exercise in using J.
For points x y : A ⊔ B in the disjoint sum / coproduct of two spaces we have that the space x ≡ y is one of the four cases
- If they are both “from A” then x ≡ y is “the same as” the corresponding path space in A
- If they are respectively from A and B then x ≡ y is “the same as” the empty space
- If they are respectively from B and A then x ≡ y is “the same as” the empty space
- If they are both “from B” then x ≡ y is “the same as” the corresponding path space in B
We go through this example in detail here.
If we have two functions f g : A → B then f ≡ g is “the same” space as (a : A) → f a ≡ g a. This is called “functional extensionality”. The HoTT proof of this is not straight forward, but in the side quests we will go through a cubical-specific proof, which is much simpler.

Univalence

Now an important question arises from these considerations :

Important

We have nice ways of describing what paths between points in constructions are, but what should paths in the space of spaces be?

Looking back on this quest (an perhaps one’s life experience) we might think “isomorphism” as it is our competing notion of “the same” for spaces. The univalence axiom says something along the lines of this :

Univalence

If two spaces are isomorphic then they are equal.

isoToPath : {A B : Type} → A ≅ B → A ≡ B

Detail

Actually univalence tends to refer to something slightly different, whilst this is a corollary of it. Refer to The HoTT Book for more details.

Hence any isomorphism we have shown can be upgraded to a path between spaces in cubical agda. For example (x ≡ y) ≡ (Id x y) can now be shown.

Quest 4 - Paths and Equality

Part 0 - The Identity Type

The construction

Exercise - Symmetry

Exercise - Transitivity

Exercise - Groupoid Laws

Recursor - The Mapping Out Property of Id

Part 1 - The Path Space

Paths versus Id

Part 2 - Properties of the Path Space

The Basics

Chains of Equalities

pathToFun

endPt

Part 3 - Univalence

Paths on Other Constructions

Univalence

Recursor - The Mapping Out Property of `Id`

Paths versus `Id`

`pathToFun`

`endPt`