Overview
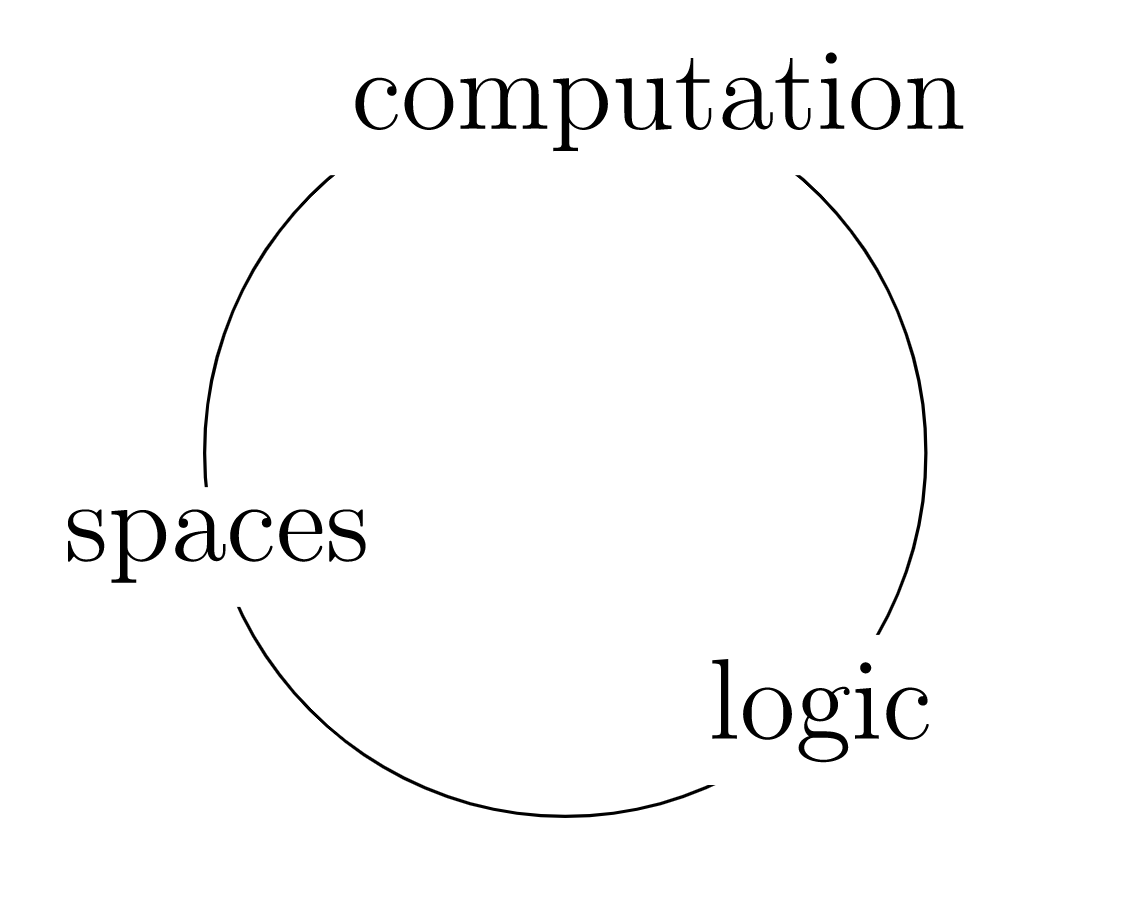
This arc introduces the setting “a place to do maths”. The “types” that will populated this “place” will have three interpretations:
Proof theoretically, with types as propositions
Type theoretically, with types as programs
Category theoretically (geometrically), with types as objects (spaces) in a category (the space of spaces)
Terms and Types
Here are some things that we could like to have in a ‘place to do maths’
objects to reason about (E.g.
ℕ)recipes for making things inside objects (E.g.
n + mfornandmin naturals.)propositions to reason with (E.g.
n = 0fornin naturals.)a notion of equality
In proof theory, types are propositions and terms of a type are their proofs. In type theory, types are programs / constructions and terms are algorithms / recipes. In category theory, types are objects (spaces) and terms are generalised elements (points in the space).
Non-dependent Types
false / empty / initial object
true / unit / terminal object
or / sum / coproduct
and / pairs / product
implication / functions / internal hom
Dependent Types
predicate / type family / bundle
substitution / substitution / pullback (of bundles)
existence / Σ type / total space of bundles
for all / Π type / space of sections of bundles
What is ‘the Same’?
The last missing piece is a notion of equality. How HoTT treats equality is where it deviates from its predecessors.