Quest 1 - Dependent Types

In a “place to do maths” we would like to be able to express and “prove” the statement

The statement

There exists a natural that is even.

The goal of this quest is to define what it means for a natural to be even.

Part 0 - Predicates / Dependent Constructions / Bundles

This requires the notion of a predicate. In general a predicate on a type A : Type is a term of type A → Type. For example,

isEven : ℕ → Type
isEven n = ?

Do C-c C-l to load the file.
Navigate to the hole.
Input n in the hole and do C-c C-c. You should now see
```
isEven : ℕ → Type
isEven zero = {!!}
isEven (suc n) = {!!}
```
It says “to define a function on ℕ, it suffices to define the function on the cases, zero and suc n, since these are the only constructors given in the definition of ℕ”. This has the following interpretations :
- propositionally, this is the principle of mathematical induction.
- categorically, this is the universal property of a natural numbers object.
Navigate to the first hole and check the goal. You should see
```
Goal: Type
———————————
```
Fill the hole with ⊤, since we want zero to be even.
Navigate to the second hole.

Input n and do C-c C-c again. You should now see

isEven : ℕ → Type
isEven zero = ⊤
isEven (suc zero) = {!!}
isEven (suc (suc n)) = {!!}

We have just used induction again.

Navigate to the first hole and check the goal. agda should be asking for a term of type Type, so fill the hole with ⊥, since we don”t want suc zero to be even.
Navigate to the next hole and check the goal. You should see in the *Agda information* window,
```
Goal: Type
——————————————
n : ℕ
```
We are in the “inductive step”, so we have access to the previous natural number.
Fill the hole with isEven n, since we want suc (suc n) to be even precisely when n is even. The reason we have access to the term isEven n is again because we are in the “inductive step”.
There should now be nothing in the *Agda information* window. This means everything is working. (Compare your isEven with our solutions in Quest2Solutions.agda.)

Part 1 - Interpretations of Bundles

The interpretations of isEven : ℕ → Type are

Propositionally : Already mentioned, isEven is a predicate on ℕ.
As a construction : isEven is a dependent construction. Specifically, isEven n is either ⊤ or ⊥ depending on n : ℕ.
Geometrically : seen as a map from the space ℕ to the space of spaces Type, isEven assigns for every point n in ℕ a space isEven n. Pictorially, it looks like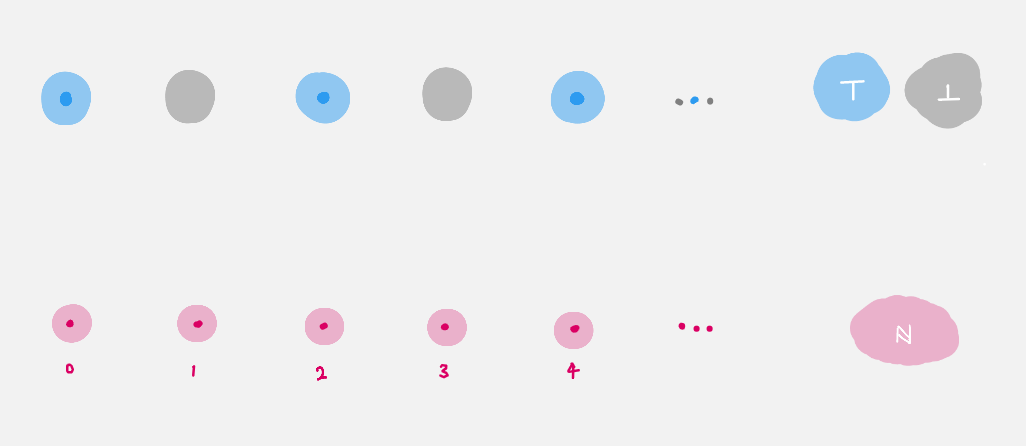

We say isEven is a bundle of spaces over ℕ, or simply a bundle over ℕ for short. The space isEven n lying above each n is called the fiber over n. In this particular example the fibers are either empty or singleton.

Note

In the above picture, we have implicitly drawn ℕ as a bunch of “disconnected” points, i.e. a discrete space. See a later arc where this is justified.
Categorically : isEven is an object in the over-category Type↓ℕ.

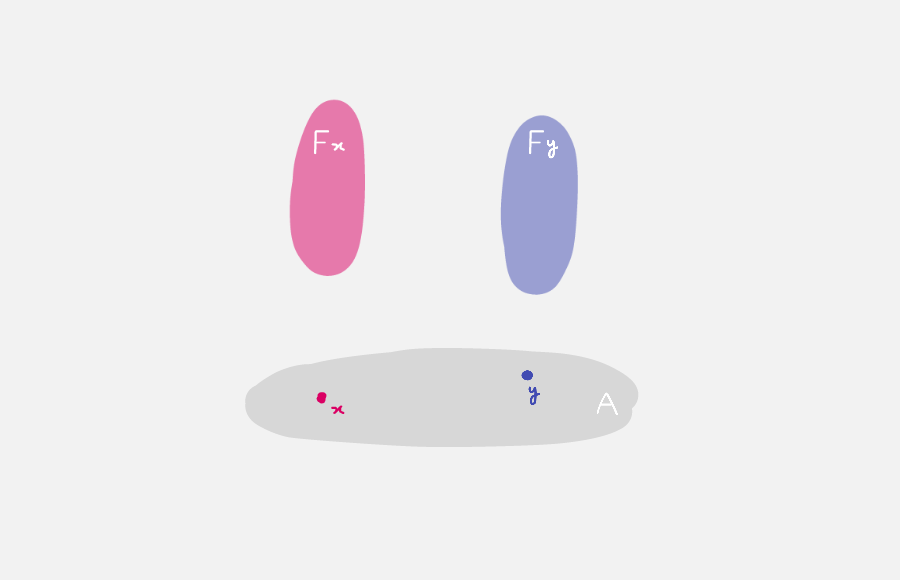
In general given a type A : Type, a dependent type F over A is a term F : A → Type. This should be drawn as a collection of space parameterised by the space A.

You can check if 2 is even by asking agda to “reduce” the term isEven 2 (do C-c C-n, “n” for normalize) and type in isEven 2. (You can write in numerals since we are now secretly using ℕ from the cubical agda library.)

Part 2 - Using the Trinitarianism

We introduced new ideas through each perspectives, as each has their own advantage

Types as propositions is often the most familiar perspective, and hence can offer guidance for the other two perspectives. However the current mathematical paradigm uses “proof irrelevance” (two proofs of the same proposition are always “the same”), which is not compatible with HoTT. We will expand on this later.
Types as constructions conveys the way in which “data” is important, and should be preserved.
Types as objects/spaces allows us to draw pictures, thus guiding us through the syntax with geometric intuition.

For each new idea introduced, make sure to justify it proof theoretically, type theoretically and categorically/geometrically.