Quest 0 - Terms and Types
There are three ways of looking at A : Type.
proof theoretically, “
Ais a proposition”type theoretically, “
Ais a construction”geometrically / categorically, “
Ais a space andTypeis the category of spaces”.
A first example of a type construction is the function type.
Given types A : Type and B : Type,
we have another type A → B : Type which can be seen as
the proposition “
AimpliesB”the construction ways to convert
Arecipes toBrecipes”the space of maps from
AtoB, i.e. maps fromAtoBcorrespond to points ofA → B.internal hom of the category
Type
To give examples of this, lets make some types first.
Part 0 - True / Unit / Terminal object
data ⊤ : Type where
tt : ⊤
It reads “⊤ is an inductive type with a constructor tt”,
with interpretations
⊤is a proposition “true” and there is a proof of it, calledtt.⊤is a construction “top” with a recipe calledtt⊤is the singleton space⊤is a terminal object: every object has a morphism into⊤given by· ↦ tt
In general, the expression a : A is read “a is a term of type A”,
and has interpretations interpretations,
ais a proof of the propositionAais a recipe for the constructionAais a point in the spaceAais a generalised element of the objectAin the categoryType.
The above tells you how we make a term of type ⊤.
Lets see an example of using a term of type ⊤:
TrueToTrue : ⊤ → ⊤
TrueToTrue = {!!}
enter
C-c C-l(this meansCtrl-c Ctrl-l). Whenever you do this,agdawill check the document is written correctly. This will open the*Agda Information*window looking like?0 : ⊤ → ⊤ ?1 : ⊤ ?2 : ⊤
This says you have three unfilled holes.
Now you can fill the first hole.
Navigate to the hole
{ }usingC-c C-f(forward) orC-c C-b(backward)Enter
C-c C-r. Therstands for refine. Whenever you do this whilst having your cursor in a hole,agdawill try to help you.You should see
λ x → { }. This isagdanotation forx ↦ { }and is calledλabstraction, think “λfor let”.Navigate to the new hole
Enter
C-c C-,(this meansCtrl-c Ctrl-comma). Whenever you make this command whilst having your cursor in a hole,agdawill check the goal.The goal (
*Agda information*window) should look likeGoal: ⊤ ————————————————————————— x : ⊤
you have a proof/recipe/generalized element
x : ⊤and you need to give a proof/recipe/generalized element of⊤Write the proof/recipe/generalized element
xof⊤in the holePress
C-c C-SPCto fill the hole withx. In general when you have some term (and your cursor) in a hole, doingC-c C-SPCwill tellagdato replace the hole with that term.agdawill give you an error if it cant make sense of your term.The
*Agda Information*window should now only have two unfilled holes left, this meansagdahas accepted your proof.?1 : ⊤ ?2 : ⊤
There is more than one proof (see Quest0Solutions.agda).
Here is an important one:
TrueToTrue' : ⊤ → ⊤
TrueToTrue' x = { }
Navigate to the hole and check the goal.
Note
xis already taken out for you.You can try type
xin the hole andC-c C-ccstands for cases”. DoingC-c C-cwithxin the hole tellsagdato do cases onx”. The only case istt.
One proof says for any term x : ⊤ give x again.
The other says it suffices to do the case of tt,
for which we just give tt.
The same”
Are these proofs “the same”? What is “the same”?
(This question is deep and should be unsettling. The short answer is that they are internally but not externally the same.)
Built into the definition of ⊤ is the way agda can make a map out of ⊤
into another type A, which we have just used.
It says to map out of ⊤ it suffices to do the case when x is tt”, or
the only proof of
⊤isttthe only recipe for
⊤isttthe only point in
⊤isttthe only one generalized element
ttin⊤
Lets define another type.
Part 1 - False / Empty / Initial object
data ⊥ : Type where
This reads “⊥ is an inductive type with no constructors”,
with interpretations
⊥is a proposition “false” with no proofs⊥is a construction “bot” with no recipes⊥is the empty spaceThere are no generalized elements of
⊥(it is a strict initial object)
We can make a map from ⊥ to any other type, in particular into ⊤.
explosion : ⊥ → ⊤
explosion x = {!!}
Navigate to the hole and do cases on
x.
agda knows that there are no cases so there is nothing to do!
(See Quest0Solutions.agda)
Our interpretations:
“false” implies “true”. In fact the same proof gives “false” implies anything (principle of explosion)
One can convert recipes of
⊥to recipes of⊤. In fact the same construction gives a recipe of any other construction since there are no recipes of⊥.There is a map from the empty space to the singleton space. In fact given any space
A, there is a map from the empty space toA.⊥is has a map into⊤. This is due to⊥being initial in the categoryType.
Part 2 - The natural numbers
We can also encode “natural numbers” as a type.
data ℕ : Type where
zero : ℕ
suc : ℕ → ℕ
Our interpretations are:
ℕhas no interpretation as a proposition since there are “too many proofs” - mathematicians classically don’t distinguish between proofs of a single proposition. (ZFC doesn’t even mention logic internally, but type theory does.) In this sense constructions are proof relevant types.As a construction :
ℕis a type of constructionzerois a recipe forℕsuctakes an existing recipe forℕand gives another recipe forℕ.
Categorically :
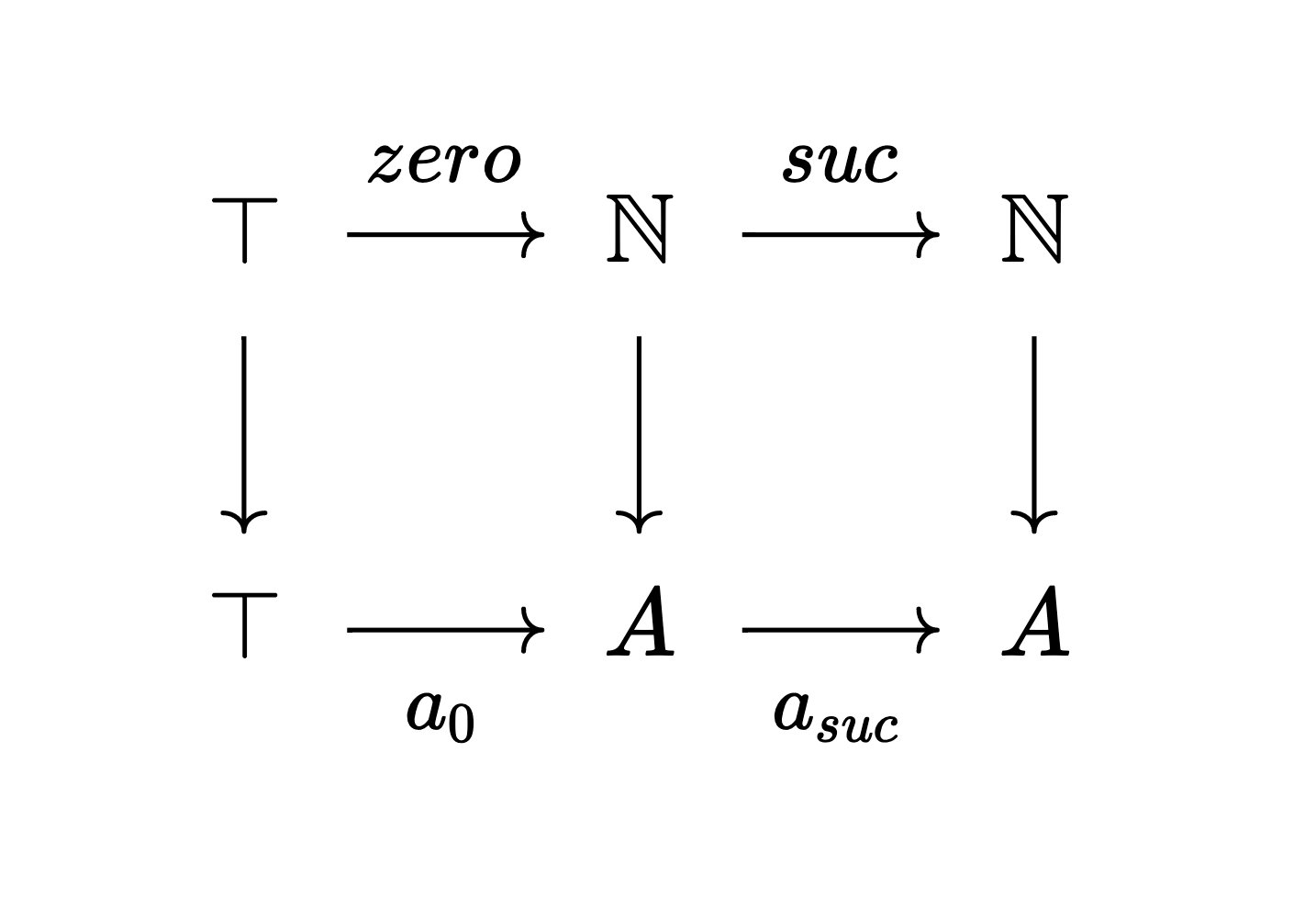
ℕis a natural numbers object in the categoryType. This means it is equipped with morphismszero : ⊤ → ℕandsuc : ℕ → ℕsuch that given any⊤ → A → Athere exist a unique morphismℕ → Asuch that the diagram commutes:
Geometrically :
ℕis a space with a pointzeroand for every pointninℕ, there is another pointsuc ninℕ.
To see how to use terms of type ℕ, i.e. to induct on ℕ,
go to Quest 1 - Dependent Types.
Part 3 - Universes
You may have noticed the notational similarities between
zero : ℕ and ℕ : Type.
The type Type has the following interpretations :
As a construction : any type of construction is a recipe for
Type.Geometrically :
Typeis a space of spaces. Each individual point inTypeis a space.
This may have lead you to the question, Type : ?.
In type theory, we simply assert Type : Type₁.
But then we are chasing our tail, asking Type₁ : Type₂.
Type theorists make sure that every type
(i.e. anything the right side of :)
itself is a term (i.e. anything on the left of :),
and every term has a type.
So what we really need is
Type : Type₁, Type₁ : Type₂, Type₂ : Type₃, ⋯
These are called universes. The numberings of universes are called levels. It will be crucial that types can be treated as terms. This will allows us to
talk about predicates i.e. “propositions depending on a variable”. E.g. the proposition “
nis even” depends on a natural numbern. See the next quest where we elaborate on this example.reason about “structures” such as “the structure of a group”, to express “for all groups, …”
do category theory without stepping out of the theory. (For experts, we have Grothendieck universes.)
reason about when two types are “the same”, for example when are two definitions of the natural numbers “the same”? What is “the same”?