Quest 0 - Working with the Circle

In this series of quests we will prove that the fundamental group of S¹ is ℤ. In fact, our strategy will also show that the higher homotopy groups of S¹ are all trivial. You don’t need to know any prerequisites - in particular we will define the fundamental group and higher homotopy groups if you don’t know what they are already.

Important

In your cloned copy of the HoTT Game locate the file 1FundamentalGroup/Quest0.agda, and open this file in emacs. Before starting it is important to have a look at our guide to emacs and list of emacs commands.

Part 0 - The Circle

Theory - Definition of the Circle

We begin by formalising the problem statement.

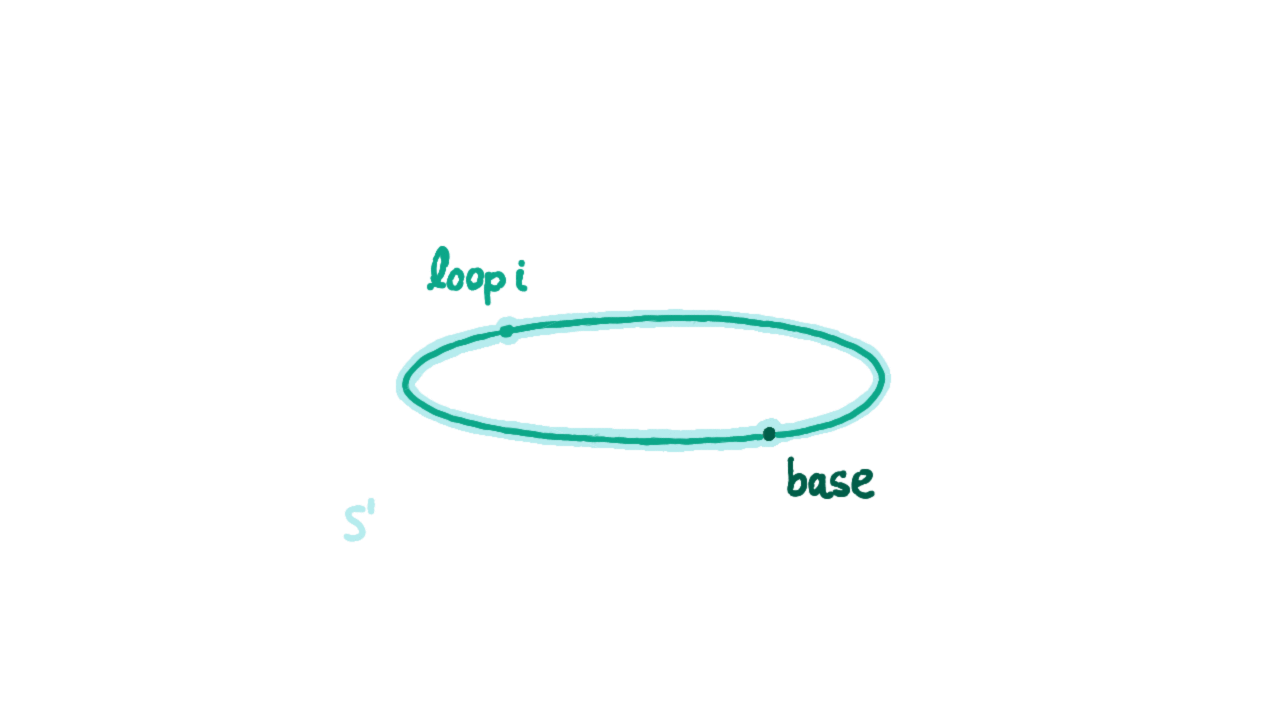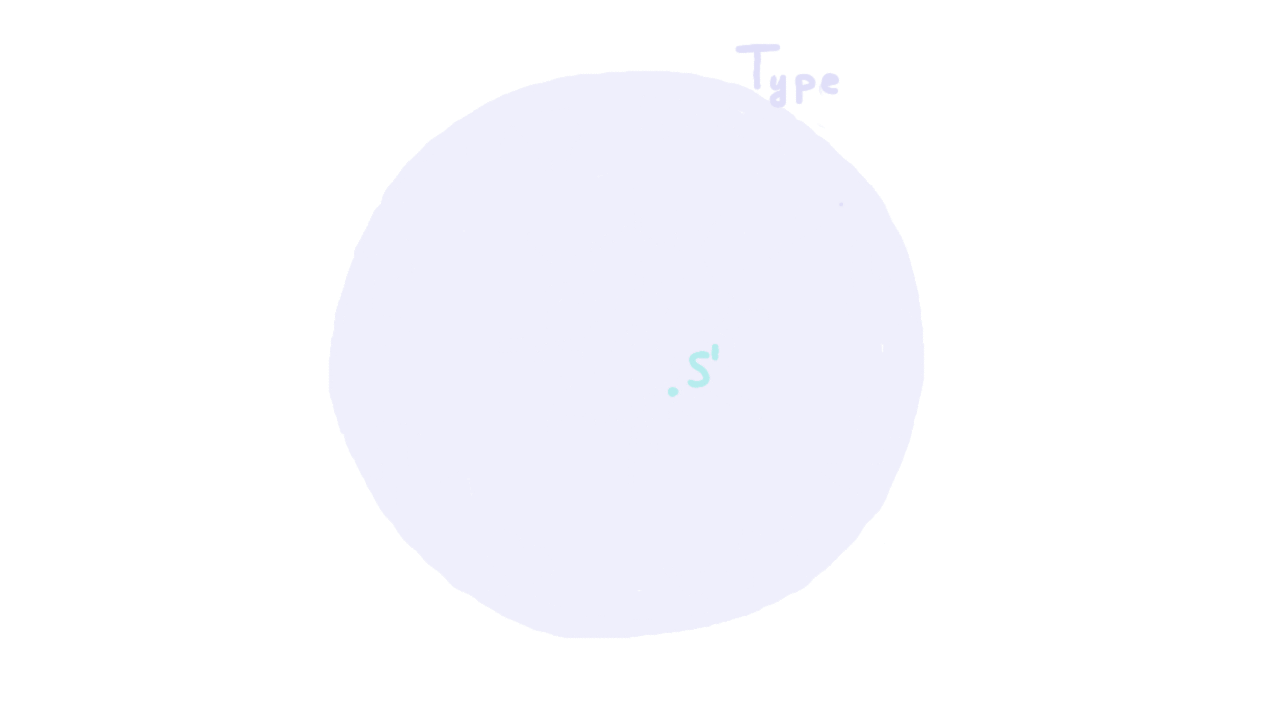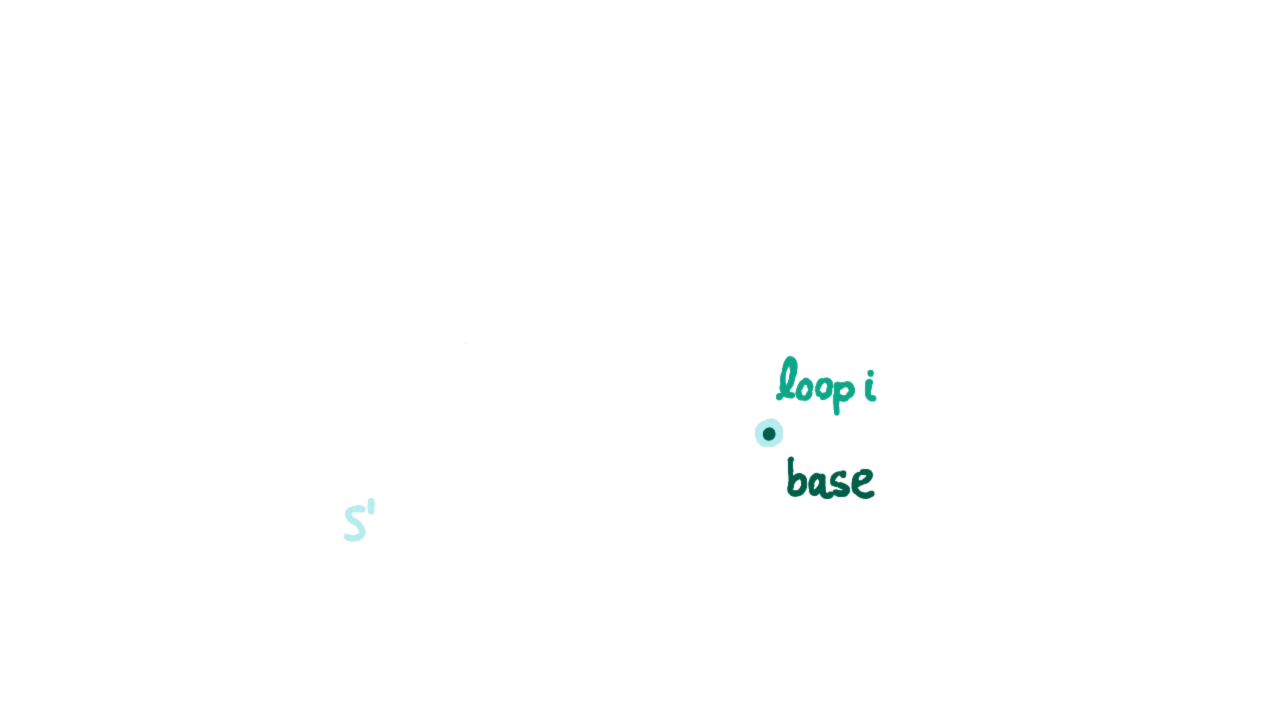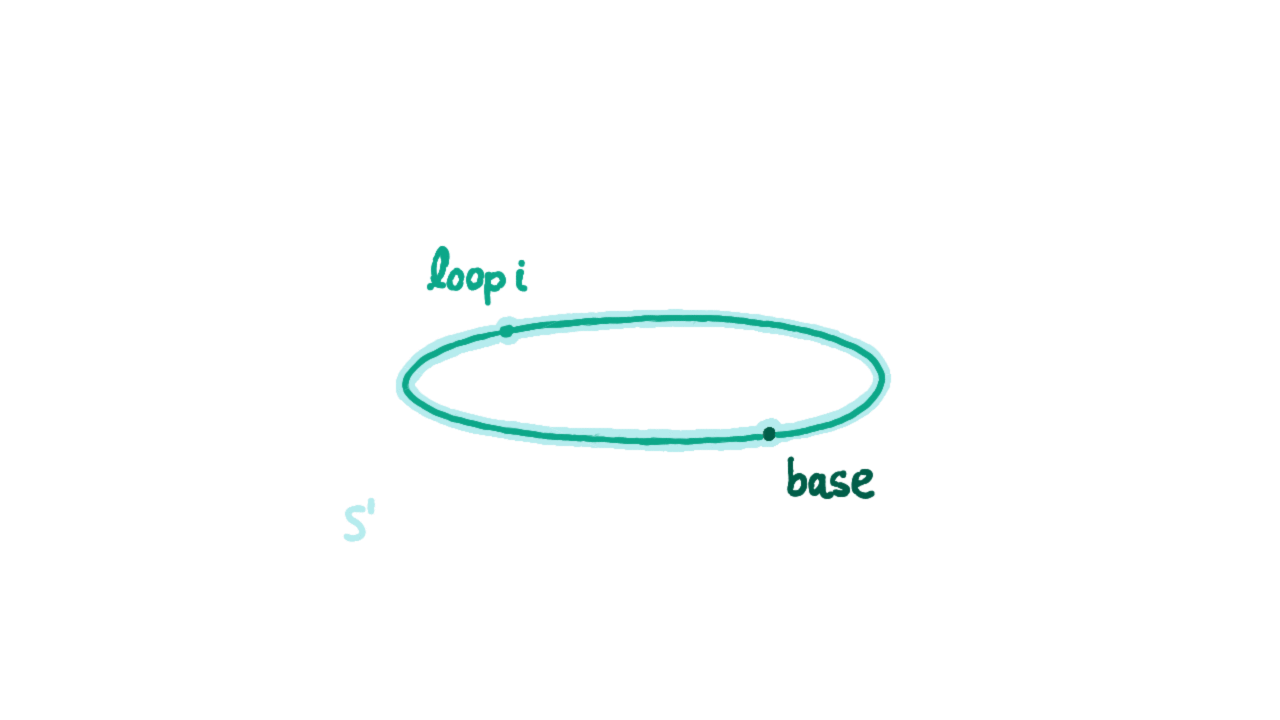
A construction of “the circle” is :

a point called base
an edge from that point to itself called loop

Here is our definition of the circle in agda.

data S¹ : Type where
  base : S¹
  loop : base ≡ base

This reads :

S¹ is a point in Type, the space of spaces. In other words, S¹ is a space.
base is a point in the space S¹
loop is a path in S¹ from base to itself. This is phrased as saying loop is a point in base ≡ base the space of paths from base to base.

Path

We think of a path in a space A as consisting of its starting point, its end point, and some generic point in the middle agreeing on the boundary.

You can see this as defining the circle via a CW-complex.

Type theory notation

In general a : A is read as a is a point in the space A. Note that in the above definition S¹ is seen both as a point and a space depending on the context. In cubical agda, everything is a point in a “unique” space.

Type theory notation

In general when a b : A (a and b are points in a space A), we have a path space a ≡ b, whose points are paths from a to b in the space A.

Exercise - defining the constant path `Refl`

There are other paths in S¹, for example the constant path at base. In 1FundamentalGroup/Quest0.agda navigate to

Refl : base ≡ base
Refl = {!!}

We will guide you through defining it. We are about to construct a path Refl : base ≡ base, a path from base to base.

Tip

The {!!} are called holes. These are blanks in the agda file that you can fill to complete the quest. You can write ? to make a new hole.

We will fill the hole Refl = {!!}.

Make sure you are in insert mode by pressing i. To escape insert mode press ESC.

Note

We have compiled a list of useful emacs and agda commands in Emacs Commands.
Enter C-c C-l (this means Ctrl-c Ctrl-l).

Whenever you do this, agda will check the document is written correctly.

We say agda compiles or loads the file. This will open the *Agda Information* window looking like

?0 : base ≡ base
?1 : (something)
?2 : (something)
...

This is the list of unfilled holes that are in your file currently. You should see that the holes in the file have changed in appearance, for example :

Refl : base ≡ base
Refl = { }0

These are what holes look like when the file is compiled. The numbering is just for reference and may change upon reloading.

Navigate between holes using C-c C-f (forward) or C-c C-b (backward).
Navigate to the first hole, making sure your cursor is inside the hole. Check the goal using C-c C-, (this means Ctrl-c Ctrl-comma). Whenever you do C-c C-,, agda will tell you what kind of “point” it expects in the hole. The *Agda Information* window should be focused on this hole only :
```
Goal: base ≡ base
```
This says agda is expecting a path from base to base in the hole. Making sure your cursor is still inside the hole, enter C-c C-r. The r stands for refine. Whenever you do this whilst having your cursor in a hole, agda will try to help you.

You should now see λ i → {!!}. This is the agda way of writing i ↦ {!!}. Load the file again (using C-c C-l) and the *Agda Information* window should now look like :

?0 : S¹
...
?6 : (something)

———— Errors ———————————————
Failed to solve the following constraints:
  ?0 (i = i1) = base : S¹ (blocked on _3)
  ?0 (i = i0) = base : S¹ (blocked on _3)

Do not worry about the errors, we will soon explain it.

Navigate (C-c C-f and C-c C-b) to that new hole in λ i → {!!} and enter C-c C-, to check the goal. The *Agda information* window should look like :
```
Goal: S¹
—————————————————————————
i : I
———— Constraints ——————————————
?0 (i = i1) = base : S¹ (blocked on _3, belongs to problem 4)
?0 (i = i0) = base : S¹ (blocked on _3, belongs to problem 4)
_4 := λ i → ?0 (i = i) (blocked on problem 4)
```
This says :
- agda is expecting a point in S¹ for this hole.
- you have a point i in I available to you. You can think of I as the “unit interval” and i as a generic point in the interval.
- The point in S¹ that you give has to satisfy the constraints that it is base when “i = 1” and “i = 0”. In agda, i0 and i1 are the “start” and “end” point of I. Afterall, we are defining a path from base to itself.
- Don’t worry about the last line.
Since Refl is meant to be the constant path at base, write base in the hole.
Press C-c C-SPC to fill the hole with base. In general when you have some text (and your cursor) in a hole, doing C-c C-SPC will tell agda to replace the hole with that text. agda will give you an error if it can’t make sense of your text.

Tip

Everytime you are filling a hole, it is recommended that you first write what you want to fill in the hole then do C-c C-SPC. You can do it in the reverse order, however the recommended order has other benefits down the line.
Load the file again (C-c C-l). The *Agda Information* window should now look like this :
```
?0 : Bool
?1 : Bool ≅ Bool
?2 : Bool ≡ Bool
?3 : Type
?4 : doubleCover base
?5 : ⊥
```
The ?0 : S¹ has disappeared. This means agda has accepted what you filled this hole with.
If you want to play around with this you reset this question by replacing what you wrote with ? and doing C-c C-l.

Part 1 - `Refl ≡ loop` is empty

To get a better feel of S¹, we show that the space of paths (homotopies) between Refl and loop, written Refl ≡ loop, is empty.

Paths between paths

In general if we have p q : a ≡ b in a space A then a path Path : p ≡ q in the path space a ≡ b consists of

the starting path p
the end path q
and some generic path in between Path i : a ≡ b that agrees on the boundary

In algebraic topology this is called a path homotopy.

First, we define the empty space and what it means for a space to be empty. Here is what this looks like in agda :

data ⊥ : Type where

This says “the empty space ⊥ is a space with no points in it”.

Here are three candidate definitions for a space A to be empty :

there is a point f : A → ⊥ in the space of functions from A to the empty space
there is a path p : A ≡ ⊥ in the space of spaces Type from A to the empty space
there is an isomorphism i : A ≅ ⊥ of spaces

These turn out to be “the same” (see Different notions of “empty”), however for our present purposes we will use the first definition. Our goal is therefore to produce a point in the function space

( Refl ≡ loop ) → ⊥

The authors of this series have thought long and hard about how one would come up with the following argument. Unfortunately, sometimes mathematics is in need of a new trick and this was one of them.

The trick

We make a path p : true ≡ false from the assumed path (homotopy) h : Refl ≡ loop by constructing a non-trivial Bool-bundle over the circle, hence obtaining a map ( Refl ≡ loop ) → ⊥.

To elaborate : Bool here refers to the discrete space with two points true, false. We will create a map doubleCover : S¹ → Type that sends base to Bool and the path loop to a non-trivial path flipPath : Bool ≡ Bool in the space of spaces.

Viewing the picture vertically, for each point x : S¹, we call doubleCover x the fiber of doubleCover over x. All the fibers look like Bool, hence our choice of the name Bool- *bundle*.

Homotopy type theory

A path p : X ≡ Y between two spaces X Y : Type (viewed as points in the space of spaces) can be visualised as follows :

Two spaces X and Y as end points.
For the generic point i : I in the interval p i : Type is a space that varies continuously with to respect to i such that p 0 is X and p 1 is Y.

The continuity guarantees that each point along the path looks “the same”. In particular the end points look “the same”.

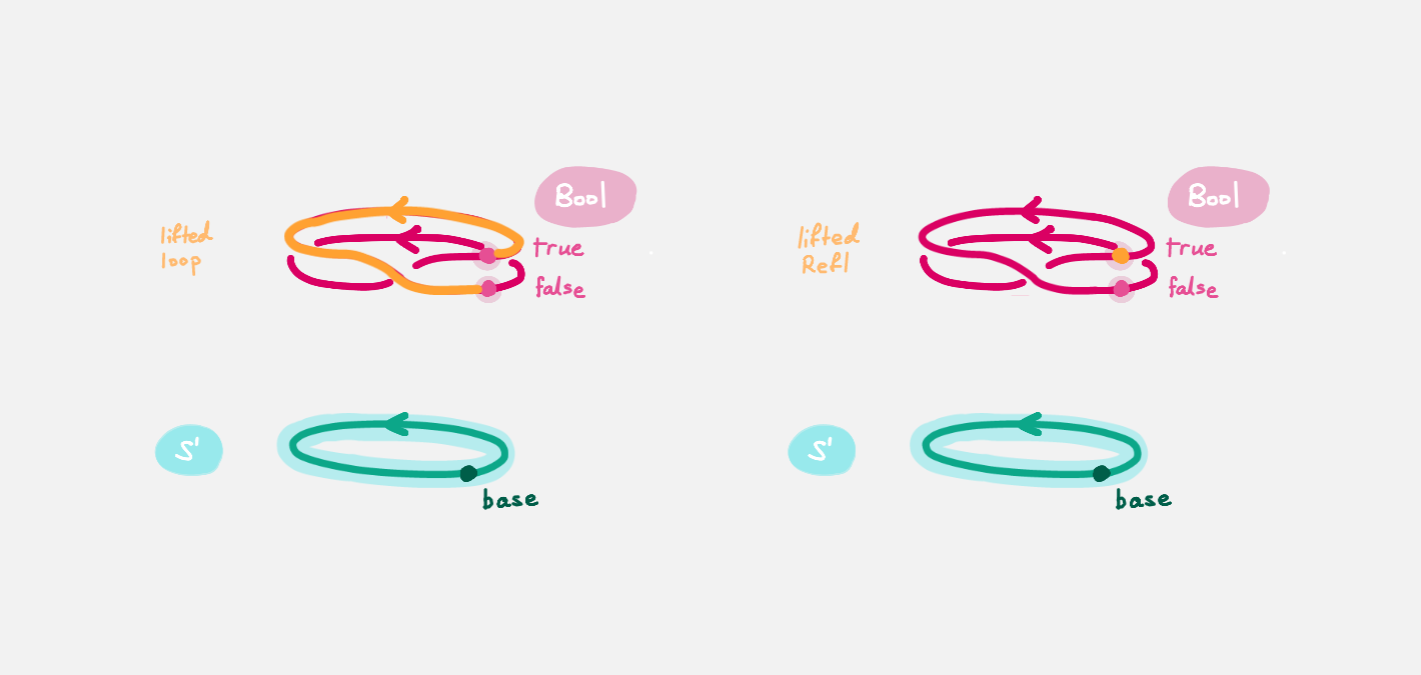
We will get a path from true to false in the fiber of doubleCover over base by “lifting the homotopy” h : Refl ≡ loop and considering the end points of the “lifted paths”. Refl will “lift” to a “constant path” and loop will “lift” to

Let’s assume for the moment that we have flipPath already and define doubleCover.

Make sure you are in insert mode.
Navigate to the definition of doubleCover and make sure you have loaded the file with C-c C-l.
```
doubleCover : S¹ → Type
doubleCover x = {!!}
```
Navigate to the hole and check the goal. It should look like
```
Goal: Type
————————————————————
x : S¹
```
This says it is expecting a point in Type, the space of spaces, i.e. it expects a space. We will first case on x by writing x in the hole and doing C-c C-c (c for cases). You should now see two new holes :
```
doubleCover : S¹ → Type
doubleCover base = {!!}
doubleCover (loop i) = {!!}
```
This means : S¹ is made from a point base and an edge loop, so a map out of S¹ to a space is the same as choosing a point to map base to, and an edge to map loop to respectively. Since loop is a path from base to itself, its image must also be a path from the image of base to itself.
Navigate to the first new hole and check the goal. We want to map base to the space Bool so write Bool in the hole, then do C-c C-SPC to fill it.
Navigate to the second new hole and check the goal. Here loop i is a generic point in the path loop, where i : I is a generic point of the “unit interval”. We are assuming we have flipPath defined already and want to map loop to flipPath, so loop i should map to a generic point in the path flipPath.

Note

We can use flipPath without completing the definition of flipPath.

Try filling the hole.
Once you think you are done, reload the agda file with C-c C-l and if it doesn’t complain this means there are no problems with your definition. Compare your definition to that in 1FundamentalGroup/Quest0Solutions.agda to check that your definition is the one we want. To navigate to solutions file escape insert mode using ESC and do SPC f f to find the file, see Emacs and Unicode Commands. Here is a definition that agda will accept, but is not what we need:
Bad definition
```
doubleCover : S¹ → Type
doubleCover base = Bool
doubleCover (loop i) = Bool
```

Defining flipPath is quite involved and we will do so in the following part.

Part 2 - Defining `flipPath` via Univalence

In this part, we will define the path flipPath : Bool ≡ Bool. Recall the picture of doubleCover.

This means we need flipPath to correspond to the unique non-identity permutation of Bool that flips true and false.

The function

We proceed in steps :

Define the function Flip : Bool → Bool.
Promote this to an isomorphism flipIso : Bool ≅ Bool.
We use univalence to turn flipIso into a path flipPath : Bool ≡ Bool. The univalence axiom asserts that paths in Type - the space of spaces - correspond to homotopy-equivalences of spaces. As a corollary, we can make paths in Type from isomorphisms in Type.

Isomorphism

One with a topological mindset might worry if isomorphism means homeomorphism, homotopy equivalence, bijection or something else; one might even wonder what continuity is here. The answer is that this is synthetic homotopy theory, where

there is no need for real numbers
every map is continuous in the sense that they respect paths
an isomorphism A ≅ B is given by the data of
- fun : A → B
- inv : B → A
- rightInv that says (extensionally) fun ∘ inv is homotopic to the identity, i.e. given any b : B we have a path fun ∘ inv b ≡ b.
- leftInv that says (extensionally) inv ∘ fun is homotopic to the identity.
You might notice that the above looks like the classical definition of homotopy equivalence. (They turn out to be “the same”.)

Univalence

We have described paths between points as giving a starting point, an ending point, and a generic point between that agrees on the boundary. Drawing a path between spaces in the space of spaces, we can see that such a path is the data of two spaces that “continuously look the same”:

We already have a notion of “the same” for spaces, which is isomorphism. Hence we assume the following “univalence” axiom : Any isomorphism can be turned into a path between spaces.

In 1FundamentalGroup/Quest0.agda, navigate to :

Flip : Bool → Bool
Flip x = {!!}

Make sure you are in insert mode.
Check the goal. It should be asking for a point in Bool, since we have already given it an x : Bool at the front.

Tip

Whenever you encounter a new hole, you should first check the goal.

Write x inside the hole, and case on x using C-c C-c with your cursor still inside. You should now see :
```
Flip : Bool → Bool
Flip false = {!!}
Flip true = {!!}
```
This means : the space Bool is made of two points false, true and nothing else, so to map out of Bool it suffices to find images for false and true respectively.
Since we want Flip to flip true and false, fill the first hole with true and the second with false.
To check things have worked, try C-c C-d (d stands for deduce its space). Then agda will ask you to input an expression. Enter Flip. In the *Agda Information* window, you should see
```
Bool → Bool
```
This means agda recognises Flip as a well-formulated term and is a point in the space of maps from Bool to Bool.
We can also ask agda to compute outputs of Flip. Try C-c C-n (n stands for normalise), agda should again be asking for an expression. Enter Flip true. In the *Agda Information* window, you should see false, as desired.

The isomorphism

Navigate to
```
flipIso : Bool ≅ Bool
flipIso = {!!}
```

Refine with C-c C-r. You should now see

flipIso : Bool ≅ Bool
flipIso = iso {!!} {!!} {!!} {!!}

Given two spaces A and B, iso (with respect to A and B) belongs to the following space :
```
iso : (fun : A → B) (inv : B → A)
      (rightInv : section fun inv) (leftInv : retract fun inv) →
      A ≅ B
```
which says that iso will produce an isomorphism from A to B given a map fun forwards and an inverse inv backwards, and points of the space section fun inv and retract fun inv. Try to find out what section and retract are by doing C-c C-n and entering their respective names. They should respectively say that inv is a right and left inverse of fun.
Check the first two holes, agda should expect functions Bool → Bool to go in both of them. This is because it is expecting a function and its inverse, respectively, so fill them with Flip and its inverse Flip.
Check the goal of the next two holes. They should be
```
section Flip Flip
```
and
```
retract Flip Flip
```
Add the following to your code (make sure you copy it exactly) :
```
flipIso : Bool ≅ Bool
flipIso = iso Flip Flip {!!} {!!} where

  rightInv : section Flip Flip
  rightInv x = {!!}

  leftInv : retract Flip Flip
  leftInv x = {!!}
```
Then load the file with C-c C-l. If agda gives an error it could be due to
1. missing spaces; agda is space sensitive
2. wrong indentation before rightInv and leftInv; agda is indentation sensitive
3. missing the where in the second line.
4. lower and upper case differences
where to use where

The where allows you to make definitions local to the current definition, in the sense that you will not be able to access rightInv and leftInv outside this proof. We will eventually fill the missing holes from before with rightInv and leftInv. If you like you can also place the definitions of rightInv and leftInv before flipIso.
Check the goal of the hole rightInv x = {!!}. In the *Agda Information* window, you should see
```
Goal: Flip (Flip x) ≡ x
—————————————————————————————————
x : Bool
```
This says rightInv should give for each x : Bool a path p : Flip (Flip x) ≡ x. We gave an x : Bool in front, so the goal is simply to give a path p : Flip (Flip x) ≡ x. Try to give such a path.

Hint
You need to case on what x can be. Then for the case of false, Flip (Flip false) should just be false by design, so you need to give a path from false to false.

The benefit of having x before the = is that we can case on what x can be. This is called pattern matching.
Do the same for leftInv x = {!!}.
Fill in the missing goals from the original problem using rightInv, leftInv.
If you got the definition right then agda should not have any errors when you load using C-c C-l.

The path

Navigate to

flipPath : Bool ≡ Bool
flipPath = {!!}

In the hole, write in isoToPath and refine with C-c C-r. You should now have
```
flipPath : Bool ≡ Bool
flipPath = isoToPath {!!}
```
If you check the new hole, you should see that agda is expecting an isomorphism Bool ≅ Bool.

isoToPath is the function from the cubical library that converts isomorphisms between spaces into paths between the corresponding points in the space of spaces Type.
Fill in the hole with flipIso and use C-c C-d to check agda is happy with flipPath.
Try to normalise pathToFun flipPath false. You should get true in the *Agda Information* window.

What pathToFun did is it took the path flipPath in the space of spaces Type and followed the point false as Bool is transformed along flipPath. The end result is of course true, since flipPath is the path obtained from flip! Try to follow what pathToFun does in the animation.

pathToFun

pathToFun is called transport in the cubical library.

Part 3 - Lifting paths using `doubleCover`

By the end of this page we will have shown that refl ≡ loop is an empty space. In 1FundamentalGroup/Quest0.agda locate

Refl≢loop : Refl ≡ loop → ⊥
Refl≢loop h = ?

The cubical library has the result true≢false : true ≡ false → ⊥ which says that the space of paths in Bool from true to false is empty. We will assume it here and leave the proof as a side quest, see Proving true≢false.

Load the file with C-c C-l and navigate to the hole. Write true≢false (input \==n for ≢; see Emacs and Unicode Commands) in the hole and refine using C-c C-r, agda knows true≢false maps to ⊥ so it automatically will make a new hole.
Check the goal in the new hole using C-c C-, it should be asking for a path from true to false.

To give this path we need to visualise “lifting” Refl, loop and the homotopy h : Refl ≡ loop along the Bool-bundle doubleCover. When we “lift” Refl - starting at the point true : doubleCover base - it will still be a constant path at true, drawn as a dot true. When we “lift” loop - starting at the point true : doubleCover base - it will look like

The homotopy h : Refl ≡ loop is “lifted” (starting at “lifted Refl”) to some kind of surface

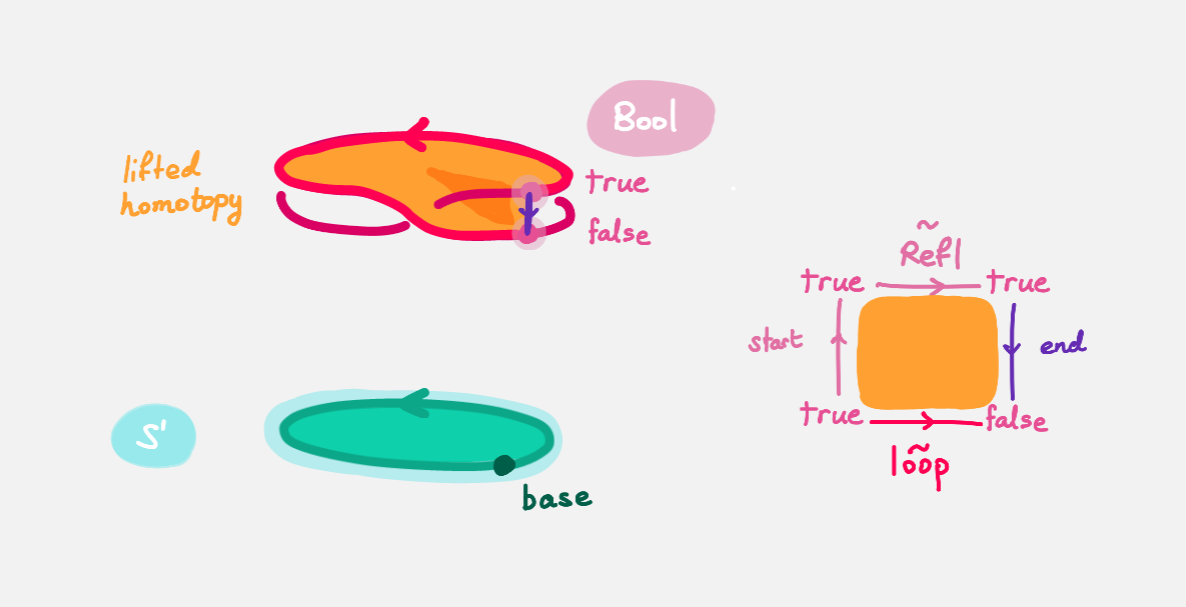
According to the pictures the end point of the “lifted” Refl is true and the end point of the “lifted” loop is false. We are interested in the end points of each “lifted paths” in the “lifted homotopy”, since this forms a path in the endpoint fiber doubleCover base from true to false.

We can evaluate the end points of both “lifted paths” by using something in the cubical library (called subst) which we call endPt.

endPt : (B : A → Type) (p : x ≡ y) (bx : B x) → B y

Note

It says given a bundle B over space A, a path p from x : A to y : A, and a point bx above x, we can get the end point of “lifted p starting at bx”. So let’s make the function that takes a path from base to base and spits out the end point of the “lifted paths” starting at true.

endPtOfTrue : base ≡ base → doubleCover base
endPtOfTrue p = {!!}

Check the goal. It should be asking for

Goal: Bool
—————————————————————————─
p : base ≡ base
———— Constraints ———————————————
?0 (p = loop) = false : Bool
  (blocked on _29, belongs to problem 90)
?0 (p = Refl) = true : Bool (blocked on _29, belongs to problem 90)
_40 := λ p i → endPtOfTrue (p i) (blocked on problem 90)

We want to use endPt, which can output something in the space B y (as described above). In this case we want B y to be Bool. agda is smart and can figure out how to use endPt :
1. Type endPt into the hole and do C-c C-r.
Tip

In general if the goal of the hole
```
Goal: Y
————————————————————————
f : X → Y
...
```
is to find a point in a space Y and you have a function f : X → Y then you can write f in the hole and do C-c C-r.
You should see
```
endPtOfTrue : base ≡ base → doubleCover base
endPtOfTrue p = endPt {!!} {!!} {!!}
```
1. Check these new holes.
2. Try to fill in these holes.
Once you think you are done, you can verify our expectation that endPtOfTrue Refl is true and endPtOfTrue loop is false using C-c C-n.

Lastly we need to make the function endPtOfTrue take the path h : Refl ≡ loop to a path from true to false. In general if f : A → B is a function and p is a path between points x y : A then we get a map cong f p from f x to f y. (Note that p here is actually a homotopy h.)

cong : (f : A → B) → (p : x ≡ y) → f x ≡ f y

We will define cong in a side quest Using cong and endPtOfTrue you should be able to complete Quest0. If you have done everything correctly you can reload agda and see that you have no remaining goals.