Quest 3 - The Loop Space is ℤ

In Quest 1 - Loop Space of the Circle we introduced our main method of proving that the fundamental group (which we take to be loopSpace S¹ base for now) is ℤ, and in Quest 2 - ℤ is a Set we decided that this means to show that they are equal spaces. .. admonition:: The Goal

loopSpace≡ℤ : loopSpace S¹ base ≡ ℤ
loopSpace≡Z = {!!}

As usual we will show this via giving an isomorphism, so we must make comparison maps forward and back. However, we discovered we had to define the backwards map over all of S¹. We already have windingNumber, the forwards comparison map, which gives us a map loopSpace S¹ base → ℤ when applied to base.

windingNumber : (x : S¹) → base ≡ x → helix x

In this quest our goal is to make a map backwards

Current Goal

rewind : (x : S¹) → helix x → base ≡ x

Since windingNumber took a path and found how many times the path loops around, in general “an integer twisted around the helix a bit”, or “an integer plus a bit”. We want to make rewind do the reverse. So rewind should take “an integer n plus a bit”, loop around n times, then add that extra corresponding bit, the path from base to x to the end.

Part 0 - rewind

Dependent paths

We try making rewind. We can assume a point x : S¹, then case on what it is.

rewind : (x : S¹) → helix x → base ≡ x
rewind base = {!!}
rewind (loop i) = {!!}

In the case of base we want a map from helix base i.e. ℤ, to base ≡ base. Try filling this in.

Solution

We want this to be the correct inverse, described as looping around n times and adding that extra bit on the end. However there is nothing to add at the end in this case, so it should just be loop_times, which we already defined in Quest 1 - Loop Space of the Circle.

The case of loop i will be a lot more work. Checking the goal we see that at each point loop i on the loop, it wants a point in the space helix (loop i) → base ≡ (loop i), which it might reduce to sucℤPath i → base ≡ (loop i) according to the definition of helix.

Collecting these spaces together along this i, we obtain a loop in the space of spaces based at the space ℤ → base ≡ base given by

λ i → helix (loop i) → base ≡ (loop i) : (ℤ → base ≡ base) ≡ (ℤ → base ≡ base).

Now collecting the points we need to give into a “path” as well, we obtain the notion of a dependent path : each point of this “path” belongs to a space along the path of spaces. We define dependent paths and design a way of mapping out of S¹ in general in Quest 5 - Dependent Paths from Trinitarianism. We assume from now on knowledge of dependent paths.

Using outOfS¹

Now that we have a way of mapping out of S¹ (using PathD), called outOfS¹D, try to use it to repackage the work we have to far.

Solution

Originally we have

rewind : (x : S¹) → helix x → base ≡ x
rewind base = loop_times
rewind (loop i) = {!!}

Now we rearrange this to

rewind : (x : S¹) → helix x → base ≡ x
rewind = outOfS¹D (λ x → helix x → base ≡ x) loop_times {!!}

since our bundle over S¹ is (λ x → helix x → base ≡ x) and our image for base is loop_times.

Checking the last goal, it remains to give a dependent path of type PathD (λ i → sucℤPath i → base ≡ loop i) loop_times loop_times. Remembering the definition of PathD, this should be exactly giving a path pathToFun (λ i → sucℤPath i → base ≡ loop i) loop_times ≡ loop_times, since PathD reduces the issue of dependent paths to just paths in the end space, which is ℤ → base ≡ base in this case. Let’s make this a chain of equalities :

Solution

rewind : (x : S¹) → helix x → base ≡ x
rewind = outOfS¹D (λ x → helix x → base ≡ x) loop_times
  (
    pathToFun (λ i → sucℤPath i → base ≡ loop i) loop_times
  ≡⟨ {!!} ⟩
    loop_times ∎
  )

Functions and pathToFun

The map loop_times takes an integer and does loop that many times. On the other hand pathToFun follows how loop_times changed along the path of spaces λ i → sucℤPath i → base ≡ loop i, and spits out the corresponding point at the end. This path of spaces is specifically a path of function spaces, so we need to find a more explicit way of describing what pathToFun does to spaces of functions.

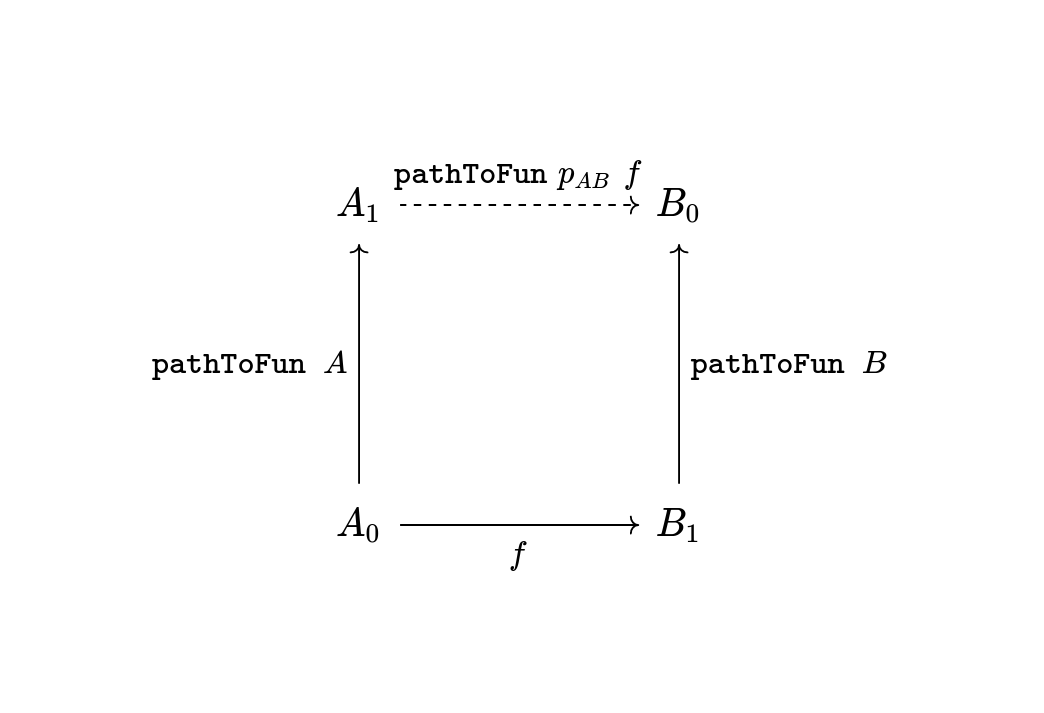
To generalize, suppose we have spaces A0 A1 B0 B1 : Type and paths A : A0 ≡ A1 and B : B0 ≡ B1. Then let pAB denote the path λ i → A i → B i : (A0 → B0) ≡ (A1 → B1). We want to figure out what pathToFun does when it follows a function f : A0 → B0 along the path pAB.

We know by functional extensionality that the function pathToFun pAB f : A1 → B1 should be determined by what it does to terms in A1, so we can assume a1 : A1. The idea is we “apply f by sending a1 back to A0”. Since pathToFun (sym A) a1 is meant to give the point in A0 that “looks like a1”, we try applying f to this point, then send it across again via the path B to the point f (pathToFun (sym A) a1) looks like in B1. We expect the outcome to be the same.

pathToFun→ : {A0 A1 B0 B1 : Type} {A : A0 ≡ A1} {B : B0 ≡ B1} (f : A0 → B0) →
  pathToFun (λ i → A i → B i) f ≡ λ a1 → pathToFun B (f (pathToFun (sym A) a1))

The proof of this in cubical agda is simply refl, so we need not even extract it as a lemma.

A cubical hack

Is actually one of the axioms asserted in cubical agda that pathToFun (λ i → A i → B i) f is externally equal to λ a1 → pathToFun B (f (pathToFun (sym A) a1)). Here we are using the cubical definition of pathToFun so we can simply give refl for its proof.

However, according the definition of pathToFun we gave in Trinitarianism, they are not externally equal but can be shown to be internally equal using J. We prove this from our own definitions here.

We interpret what this result means in our specific case : We are making pathToFun (λ i → sucℤPath i → base ≡ loop i) loop_times into another map in the space ℤ → base ≡ base, by following along the diagram

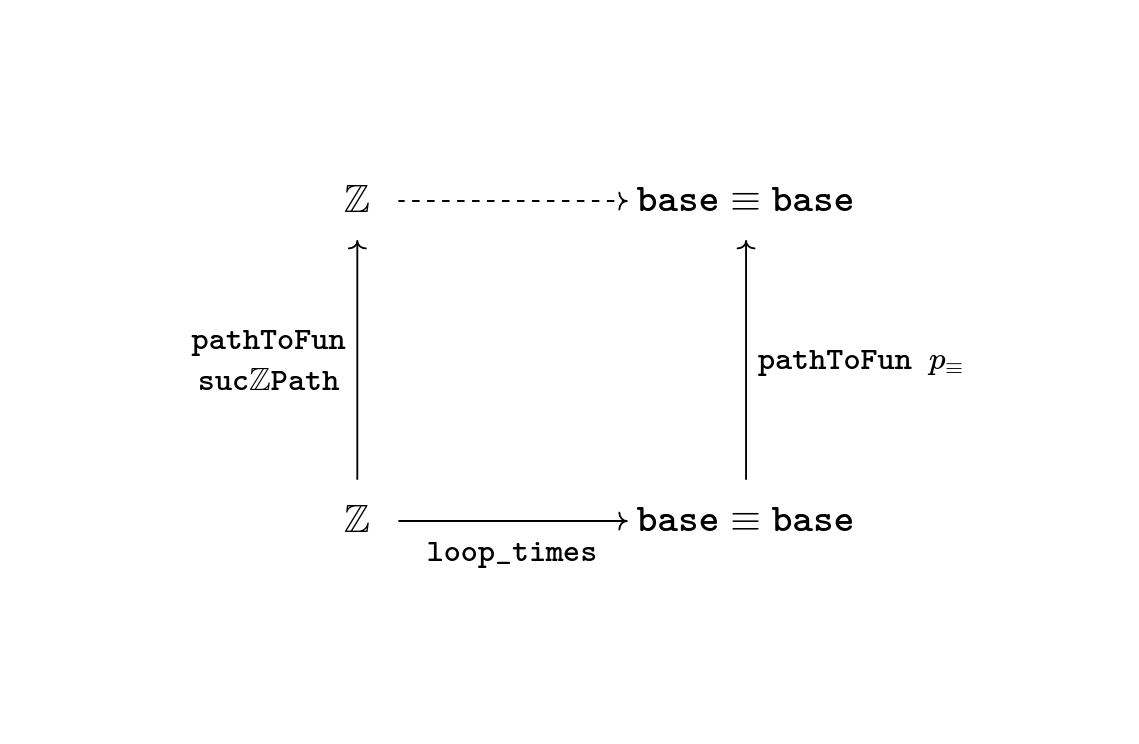
Specifically, this map should take n : ℤ and first send it backwards along sucℤPath, supposedly giving us n - 1. Then it applies loop_times, obtaining the loop loop (n - 1) times. Lastly it follows loop (n - 1) times along the path λ i → base ≡ loop i (which itself is a loop starting and ending at base ≡ base in the space of spaces), obtaining some path from base ≡ base, which we expect to be internally equal to loop n times.

Try putting this together in our definition of rewind, as a new intermediate step in our chain of equalities.

Solution

rewind : (x : S¹) → helix x → base ≡ x
rewind = outOfS¹D (λ x → helix x → base ≡ x) loop_times
  (
    pathToFun (λ i → sucℤPath i → base ≡ loop i) loop_times
  ≡⟨ refl ⟩
    (λ n → pathToFun (λ i → base ≡ loop i) (loop_times (pathToFun (sym sucℤPath) n)))
  ≡⟨ {!!} ⟩
    loop_times ∎
  )

We can simplify the above expression. We know that pathToFun (sym sucℤPath) n should follow n along sucℤPath backwards, so it should be n - 1. We can use this to move a step closer to the goal.

Solution

This equality is definitional.

rewind : (x : S¹) → helix x → base ≡ x
rewind = outOfS¹D (λ x → helix x → base ≡ x) loop_times
  (
    pathToFun (λ i → sucℤPath i → base ≡ loop i) loop_times
  ≡⟨ refl ⟩
    (λ n → pathToFun (λ i → base ≡ loop i) (loop_times (pathToFun (sym sucℤPath) n)))
  ≡⟨ refl ⟩
    (λ n → pathToFun (λ i → base ≡ loop i) (loop (predℤ n) times))
  ≡⟨ {!!} ⟩
    loop_times ∎
  )

The path fibration and pathToFun

It remains to find out how pathToFun interacts with the path of loops coming out of base. We call “the path of loops coming out of base” λ i → base ≡ loop i the path fibration at base. The animation tells us that we are gradually concatenating the input loop (n - 1) times with loop. Hence we should obtain loop (n - 1) times ∙ loop. We are a bit lucky here, and these are in fact definitionally equal, but to justify this in general, we can prove that “following along the path fibration is the same as concatenating”.

pathToFunPathFibration : {A : Type} {x y z : A} (q : x ≡ y) (p : y ≡ z) →
  pathToFun (λ i → x ≡ p i) q ≡ q ∙ p

This is in fact a quick exercise.

Hint

We take the propositional perspective - without loss of generality we can assume y and z are exactly the same.

Crucially : we know what pathToFun does to refl (recall pathToFunRefl from the quest on paths).

Solution

pathToFunPathFibration : {A : Type} {x y z : A} (q : x ≡ y) (p : y ≡ z) →
  pathToFun (λ i → x ≡ p i) q ≡ q ∙ p
pathToFunPathFibration {A} {x} {y} q = J (λ z p → pathToFun (λ i → x ≡ p i) q ≡ q ∙ p)
  (
    pathToFun refl q
  ≡⟨ pathToFunRefl q ⟩
    q
  ≡⟨ ∙Refl q ⟩
    q ∙ refl ∎
  )

To include this in rewind we have

Spoiler

rewind : (x : S¹) → helix x → base ≡ x
rewind = outOfS¹D (λ x → helix x → base ≡ x) loop_times
  (
    pathToFun (λ i → sucℤPath i → base ≡ loop i) loop_times
  ≡⟨ refl ⟩ -- how pathToFun interacts with →
    (λ n → pathToFun (λ i → base ≡ loop i) (loop_times (pathToFun (sym sucℤPath) n)))
  ≡⟨ refl ⟩ -- sucℤPath is just taking successor, and so its inverse is definitionally taking predecessor
    (λ n → pathToFun (λ i → base ≡ loop i) (loop_times (predℤ n)))
  ≡⟨ funExt (λ n → pathToFunPathFibration _ _) ⟩ -- how pathToFun interacts with the "path fibration"
    (λ n → (loop (predℤ n) times) ∙ loop)
  ≡⟨ {!!} ⟩
    loop_times ∎
  )

There are several ways to complete this final part. We will leave the rest in a hint.

Hint

Applying functional extensionality we just need to show that for each n : ℤ the outputs are equal, i.e. loop predℤ n times ∙ loop ≡ loop n times. By our design of loop_times we should have that loop m times ∙ loop is equal to loop (m + 1) times. Then we are reduced to showing that loop (sucℤ predℤ n) times ≡ loop n times, or just sucℤ predℤ n ≡ n.

Solution

rewind : (x : S¹) → helix x → base ≡ x
rewind = outOfS¹D (λ x → helix x → base ≡ x) loop_times
  (
    pathToFun (λ i → sucℤPath i → base ≡ loop i) loop_times
  ≡⟨ refl ⟩ -- how pathToFun interacts with →
    (λ n → pathToFun (λ i → base ≡ loop i) (loop_times (pathToFun (sym sucℤPath) n)))
  ≡⟨ refl ⟩ -- sucℤPath is just taking successor, and so its inverse is definitionally taking predecessor
    (λ n → pathToFun (λ i → base ≡ loop i) (loop_times (predℤ n)))
  ≡⟨ funExt (λ n → pathToFunPathFibration _ _) ⟩ -- how pathToFun interacts with the "path fibration"
    (λ n → (loop (predℤ n) times) ∙ loop)
  ≡⟨ funExt (λ n →
       loop predℤ n times ∙ loop
      ≡⟨ loopSucℤtimes (predℤ n) ⟩
        loop (sucℤ (predℤ n)) times
      ≡⟨ cong loop_times (sucℤPredℤ n) ⟩
        loop n times ∎) ⟩
    loop_times ∎
  )

We can check that rewind base is indeed loop_times by using C-c C-n. This is to be expected as outOfS¹ evaluated at base should back exactly what we fed it, as mentioned in the discussion on mapping out of the circle.

Part 1 - rewind is a right inverse

We are now in a position to approach the main goal :

loopSpaceS¹≡ℤ : loopSpace S¹ base ≡ ℤ
loopSpaceS¹≡ℤ = {!!}

We have reduced this to giving an isomorphism, which involves giving the map windingNumber base forward and loop_times backwards, and showing that they are inverses of each other.

Hence the next step is to show that “looping n times then taking the winding number gives back n”. Try to state and prove this in 1FundamentalGroup/Quest3.agda. In the hints we will use intuitive notation for integers that may not align exactly with agda code.

The statement

windingNumberRewindBase : (n : ℤ) → windingNumber base (rewind base n) ≡ n
windingNumberRewindBase = {!!}

We identify rewind base with loop_times, since they are externally equal.

Hint 0

Since loop_times was defined by casing on n we case on n - it could be zero, a positive integer, negative one, or less than negative one.

Hint 1

Some of the cases are trivial - we know exactly what loop 0 times and windingNumber base loop are.

Solution for Hint 1

windingNumberRewindBase : (n : ℤ) → windingNumber base (rewind base n) ≡ n
windingNumberRewindBase (pos zero) = refl
windingNumberRewindBase (pos (suc n)) = {!!}
windingNumberRewindBase (negsuc zero) = refl
windingNumberRewindBase (negsuc (suc n)) = {!!}

Hint 2

We can identify windingNumber base with its definition, reducing the problem to showing that endPt helix (loop n times) 0 is equal to n, in the separate cases.

For the first case, we can reduce loop (n + 1) times to just loop n times ∙ loop since that was the definition. Hence we are interested in what endPt helix (loop n times ∙ loop) 0 is. Recalling our intuition behind endPt, this amounts to following the point 0 up the helix along the path loop n times ∙ loop. This should just be going to endPt helix (loop n times) 0 then adding 1.

You can also check what agda reduces the expression to by writing it in the hole and then doing C-c C-n. It should look something like sucℤ (transp (λ i → helix (loop pos n times i)) i0 (pos 0)). Clearly it has reduced the definition a bit too far, but the important idea is there, that it is + 1 of whatever data we have already.

Lastly we can just take sucℤ on both sides of an equality we have from the induction hypothesis.

Solution

For one of the cases we detail the thought process going on above, and for the last case we extract only the important part of the proof.

windingNumberRewindBase : (n : ℤ) → windingNumber base (rewind base n) ≡ n
windingNumberRewindBase (pos zero) = refl
windingNumberRewindBase (pos (suc n)) =
    windingNumber base (rewind base (pos (suc n)))
  ≡⟨ refl ⟩
    windingNumber base (loop (pos n) times ∙ loop)
  ≡⟨ refl ⟩
    endPt helix (loop (pos n) times ∙ loop) (pos zero)
  ≡⟨ refl ⟩
    sucℤ (endPt helix (loop (pos n) times) (pos zero))
  ≡⟨ cong sucℤ (windingNumberRewindBase (pos n)) ⟩
    sucℤ (pos n)
  ≡⟨ refl ⟩
    pos (suc n) ∎
windingNumberRewindBase (negsuc zero) = refl
windingNumberRewindBase (negsuc (suc n)) = cong predℤ (windingNumberRewindBase (negsuc n))

You might wonder if it is possible to make the above map work across all of S¹, and the answer is yes. This is not really necessary for our goal, so feel free to skip to the next part if you are not interested. Try stating and proving the generalization of the above; which we call windingNumberRewind.

The Statement

windingNumberRewind : (x : S¹) (n : helix x) → windingNumber x (rewind x n) ≡ n
windingNumberRewind = {!!}

Hint 0

We defined rewind by casing on points in the circle and rewind is the first function being applied, so it would make sense to case on points in the circle. In the case when the point is base we can just give the map we wanted to generalize in the first place.

Solution to Hint 0

windingNumberRewind : (x : S¹) (n : helix x) → windingNumber x (rewind x n) ≡ n
windingNumberRewind =
  outOfS¹D (λ x → (n : helix x) → windingNumber x (rewind x n) ≡ n)
    windingNumberRewindBase {!!}

Hint 1

Checking the last hole we see that we need to give a dependent path from windingNumberRewindBase to itself. According to the definition of a dependent path, this is just a path in the last fiber from pathToFun of windingNumberRewindBase to windingNumberRewindBase (the fiber is (n : ℤ) → windingNumber base (rewind base n) ≡ n). Now this might seem very complicated : even after applying functional extensionality (this is equality of two functions) this would be “finding a path between paths in ℤ”. Try repeating that last bit in your head a couple of times.

Hint 2

We put a lot of effort into showing that ℤ is a set.

Solution

windingNumberRewind : (x : S¹) (n : helix x) → windingNumber x (rewind x n) ≡ n
windingNumberRewind = -- must case on x / use recursor / outOfS¹ since that is def of rewind
  outOfS¹D (λ x → (n : helix x) → windingNumber x (rewind x n) ≡ n)
    windingNumberRewindBase (
      pathToFun
        (λ i → (n : helix (loop i)) → windingNumber (loop i) (rewind (loop i) n) ≡ n)
        windingNumberRewindBase
    ≡⟨ funExt (λ x → isSetℤ _ _ _ _ ) ⟩
      windingNumberRewindBase ∎)

Part 2 - rewind is a left inverse

Try to show that rewind is a left inverse.

The Statement

Just like we struggled to only define windingNumber base without access to the entire circle, we make sure to include all the data we have access to. Note that this was not the case before.

rewindWindingNumber : (x : S¹) (p : base ≡ x) → rewind x (windingNumber x p) ≡ p
rewindWindingNumber x = {!!}

Hint 0

Remembering that windingNumber x p is externally equal to endPt helix p 0, and that endPt is defined by path induction - using J (this is not exactly true for endPt from the library for cubical reasons), the obvious thing to do here is to do path induction.

Solution for Hint 0

rewindWindingNumber : (x : S¹) (p : base ≡ x) → rewind x (windingNumber x p) ≡ p
rewindWindingNumber x = J (λ x p → rewind x (windingNumber x p) ≡ p) {!!}

Hint 1

It suffices to show that rewind x (windingNumber x refl) ≡ refl, which by reducing the left side is the same as showing loop_times (endPt helix refl 0) ≡ refl.

Solution to Hint 1

rewindWindingNumber : (x : S¹) (p : base ≡ x) → rewind x (windingNumber x p) ≡ p
rewindWindingNumber x = J (λ x p → rewind x (windingNumber x p) ≡ p)
     (rewind base (windingNumber base refl)
   ≡⟨ refl ⟩
     loop_times (endPt helix (refl {x = base}) (pos zero))
   ≡⟨ {!!} ⟩
     refl ∎)

Hint 2

We know what endPt does to refl, which is given by the result endPtRefl. If you need to recall what endPtRefl proves you can type it into the hole and do C-c C-. for the goal and the type of endPtRefl.

Solution to Hint 2

rewindWindingNumber : (x : S¹) (p : base ≡ x) → rewind x (windingNumber x p) ≡ p
rewindWindingNumber x = J (λ x p → rewind x (windingNumber x p) ≡ p)
     (rewind base (windingNumber base refl)
   ≡⟨ refl ⟩
     loop_times (endPt helix (refl {x = base}) (pos zero))
   ≡⟨ cong loop_times (cong (λ g → g (pos zero)) (endPtRefl {x = base} helix)) ⟩
     loop (pos zero) times
   ≡⟨ {!!} ⟩
     refl ∎)

Solution

The last step is simply remembering how loop_times computes.

rewindWindingNumber : (x : S¹) (p : base ≡ x) → rewind x (windingNumber x p) ≡ p
rewindWindingNumber x = J (λ x p → rewind x (windingNumber x p) ≡ p)
     (rewind base (windingNumber base refl)
   ≡⟨ refl ⟩
     loop_times (endPt helix (refl {x = base}) (pos zero)) -- reduce both definitions
   ≡⟨ cong loop_times (cong (λ g → g (pos zero)) (endPtRefl {x = base} helix)) ⟩
     loop (pos zero) times
   ≡⟨ refl ⟩
     refl ∎)

Part 3 - The Loop Space is ℤ

We can conclude our main goal now, by collecting all of the components we have made above. We leave you the pleasure.

Solution

As usual we construct an isomorphism, but we can choose to do this over the entire circle or just between loopSpace S¹ base and ℤ. We do the former and have the latter as a corollary, but you could just do the latter directly as well.

pathFibration≡helix : (x : S¹) → (base ≡ x) ≡ helix x
pathFibration≡helix x =
  isoToPath (iso (windingNumber x) (rewind x) (windingNumberRewind x) (rewindWindingNumber x))

loopSpaceS¹≡ℤ : loopSpace S¹ base ≡ ℤ
loopSpaceS¹≡ℤ = pathFibration≡helix base

What now?

We have mentioned already that we aren’t exactly working with the fundamental group, but the loop space. In the final quest of this arc we discuss the definition of the fundamental group and show that the loop space in this case is the fundamental group already.